材料力学において、物質の変形や応力に関する理解は非常に重要です。「ポアソン比」と「ひずみ」は、材料の挙動を理解する上で欠かせない概念です。
ポアソン比は材料が引っ張られたときにどのように材料が変形するかを示す指標であり、ひずみはその変形度合いを示す具体的な測定値です。
本記事ではそのポアソン比の定義や計算方法、ひずみとの関連性についてわかりやすく解説します。
材料力学を学び始めたばかりの方や実際の応用に役立てたい方にとって、基礎知識を深める良い機会となるでしょう。
それではさっそくポアソン比とひずみの世界を探っていきましょう。
ひずみとは?
『ひずみ』という言葉は、材料力学を学ぶ際に初めて耳にすることが多いのではないでしょうか。
ひずみとは何かというと、簡単に言えば変形の大きさを示す数値です。そして、重要なのはそれが変形の割合を示しているということです。
ひずみは縦ひずみと横ひずみ、せん断ひずみがあります。まずは横ひずみについて解説します。
横ひずみ
横ひずみ(よこひずみ)とは材料に力(荷重)がかかったときに、荷重の方向と垂直な方向に生じる変形の割合を指します。
例えば、引張力がかかると材料は縦方向に伸びますが、その際に横方向には縮むことになります。この横方向の変形のことを横ひずみと呼びます。
横ひずみはε’と表します。ひずみは無次元なので、単位はありません。(後述する縦ひずみ、せん断ひずみも同じです。)
横ひずみの求め方は材料の断面積によって決まる
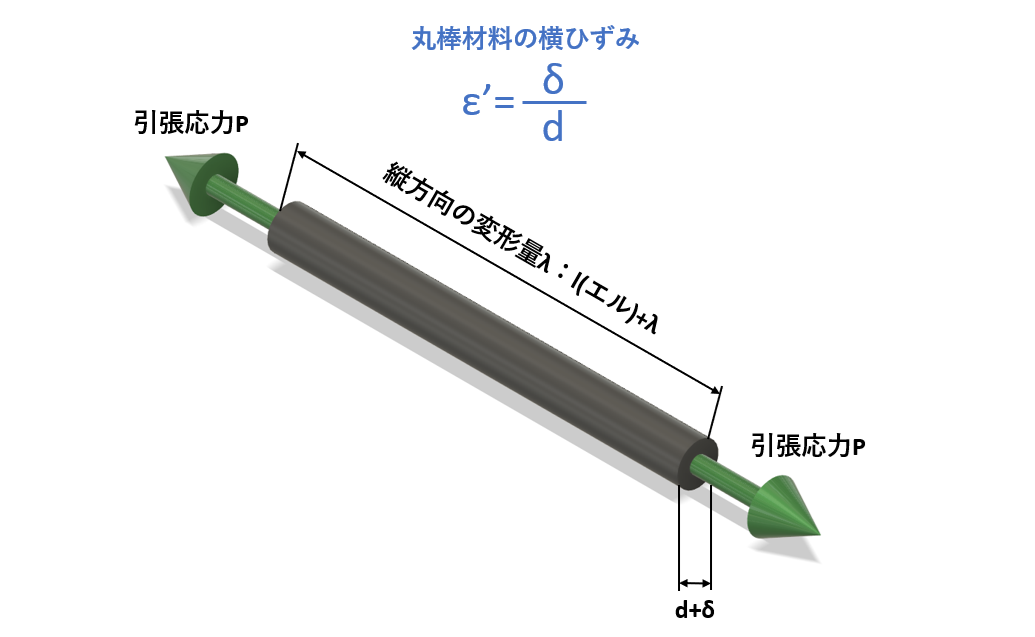
横方向の変形量をδ(デルタ)とし、円形材料の断面積をdと置いたとき、横ひずみ ε’は以下の式で表されます。
$$ε’=\frac{δ}{d}$$
ε’:横ひずみ
δ:材料の変形量
d:断面積
材料が角材の場合、縦と横2方向の変化量を考えなければいけないため、2つの横ひずみを表します。
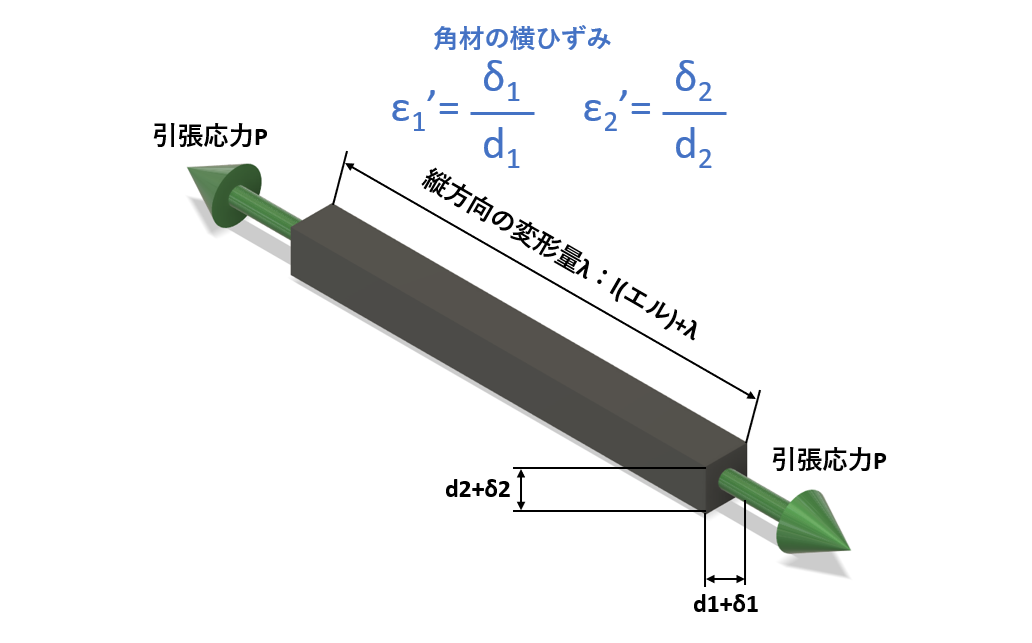
$$ε_{1}’=\frac{δ_{1}}{d_{1}}$$
$$ε_{2}’=\frac{δ_{2}}{d_{2}}$$
ε1、ε2:横ひずみ
δ1、δ2:材料の変形量
d1、d2:断面積
縦ひずみ
縦ひずみ(たてひずみ)とは物体が外力を受けたときに、その力の方向(軸方向)に沿って生じる変形の割合を指します。
具体的には物体の元の長さに対してどれくらい伸びたり縮んだりしたかを表しています。
縦ひずみは、ギリシャ文字のε(イプシロン)で表され、次の式で計算されます。
$$ε=\frac{λ}{l}$$
せん断ひずみ
せん断荷重を受ける場合はせん断ひずみというものが発生します。
せん断ひずみとは、物体にせん断応力がかかることによって生じるひずみです。
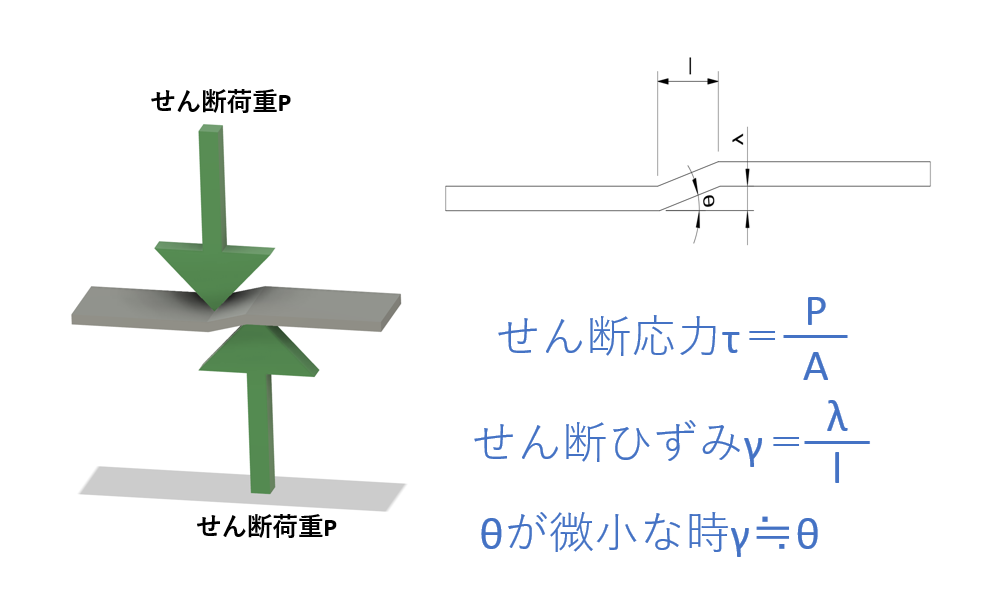
せん断荷重を受ける弾性材料も、軸方向に加わる力と同様に応力ーひずみの比例関係が成り立ち、せん断ひずみγ(ガンマ)という記号を使って表します。式は次の通りです。
$$γ=\frac{λ}{l} ・・・(1)$$
材料がせん断荷重を受けた際のせん断応力は
$$τ=\frac{P}{A} ・・・(2)$$
となり、この時せん断荷重によって生じた変位θ(rad)が微小な場合、
$$γ≒θ ・・・(3)$$
と近似することができます。
横弾性係数Gは
$$G=\frac{τ}{γ} ・・・(4)$$
であり、式(4)に式(1)と式(2)を代入すると、
$$G=\frac{τ}{γ}=\frac{\frac{P}{A}}{\frac{λ}{l}}=\frac{Pl}{Aλ}$$
が得られます。
ここで、式(3)はせん断荷重によって材料のしなる角度が著しく低い場合、γ≒θと近似できるので、式(4)の横弾性係数Gの式は以下のような関係式になります。
$$G=\frac{τ}{γ}=\frac{τ}{θ}$$
縦ひずみと横ひずみの符号
縦ひずみと横ひずみそれぞれのひずみの作用方向をまとめると以下のようになります。
| 縦ひずみ(λ、ε) | 横ひずみ(δ、ε’) | |
| 引張荷重 | +(伸びる) | -(細くなる) |
| 圧縮荷重 | -(縮む) | +(太くなる) |
材料の寸法の長さが変形によって増加するほうが+、と覚えるとわかりやすいかと思います。
ポアソン比について
もう一つ、縦ひずみと横ひずみを扱う問題で大切な考え方があります。それはポアソン比です。
ポアソン比(ν:ニュー)とは、横ひずみと縦ひずみの比率のことをいい、材料によって決まる固有定数です。おおよそ3分の1程度の数値をとることが多いです。
ポアソン比は縦ひずみと横ひずみを使って次のように定義されます。
$$ポアソン比ν=\frac{ε’}{ε}$$
ε’:横ひずみ
ε:縦ひずみ
また、ポアソン比の逆数
$$\frac{1}{ν}$$
をポアソン数と呼び、記号はmで表します。
$$m=\frac{1}{ν}$$
弾性係数とポアソン比の関係
縦弾性係数E、横弾性係数G、ポアソン比ν(ニュー)の間には、次のような関係式が成り立ちます。
$$E=2G(1+ν)$$
身近にあるポアソン比
一つの例として、ゴムバンドを引っ張る時を想像してみましょう。
ゴムバンドを引っ張ると縦に伸び(縦ひずみが発生)、同時にゴムバンドは横に縮みます(横ひずみが発生)。
このとき、縦にどれだけ伸びたか(縦ひずみ)と横にどれだけ縮んだか(横ひずみ)の比率がポアソン比です。ゴムのような材料では、この比率が約0.5に近くなります。
計算問題
例題1
直径50mm、長さ0.5mの丸棒に30kNの引張荷重を与えた。材料の縦弾性係数206GPa、ポアソン比1/3としたときの縦方向の伸びと横方向の圧縮量、縦ひずみ、横ひずみを求めなさい。
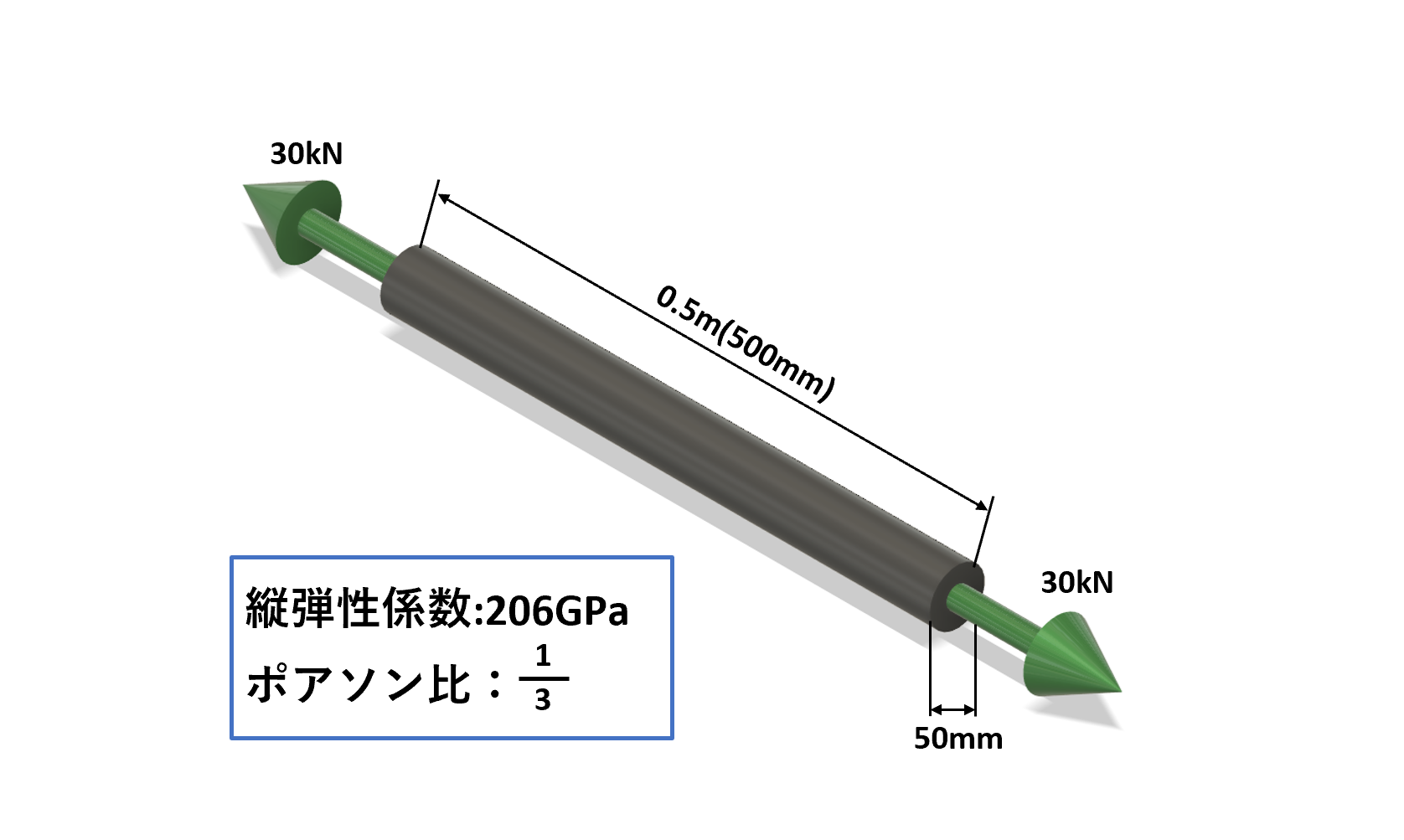
ポイント
縦ひずみ、横ひずみ、横方向の圧縮量は縦方向の伸び(λ)がわからないと求めることができないため、先に縦方向の伸びをやっつけます。縦ひずみ→横ひずみ→横方向の圧縮量の順にそれぞれの式に当てはめて解いていくと簡単に計算できます。
例題1の解答
最初に丸棒の縦方向の伸びを求めます。
縦方向の伸び
$$λ=\frac{Pl}{AE}$$
$$=\frac{\frac{Pl}{1}}{\frac{πd^2E}{4}}$$
$$=\frac{4Pl}{πd^2E}$$
$$=\frac{4×30×10^3×500}{π×50^2×206×10^3}$$
$$=0.04mm$$
次に縦ひずみを求めます。
縦ひずみ
$$ε=\frac{λ}{l}$$
$$=\frac{0.04}{500}$$
$$=0.00008=0.08×10^{-3}$$
横ひずみを求めます。
横ひずみ
$$ν=\frac{ε’}{ε}$$
$$ε’=νε=\frac{1}{3}×0.08×10^{-3}$$
$$=0.000027=0.27×10^{-4}$$
最後に横方向の圧縮量を求めます。
横方向の圧縮量(丸棒の場合)
$$ε’=\frac{δ}{d}$$
$$δ=ε’d$$
$$=0.27×10^{-4}×50$$
$$=0.00135=1.35×10^{-3}mm$$
解
縦方向の伸び:0.04mm
縦ひずみ:0.08×10-3
横ひずみ:0.27×10-4
横方向の圧縮量:1.35×10-3mm
例題2
断面積30mm×60mmのある材料で20kNのせん断荷重が作用している。横弾性係数80GPaとして、この時のせん断ひずみを求めなさい。
例題2の解答
横弾性係数
$$G=\frac{τ}{γ} ・・・(1)$$
を使ってせん断ひずみγを求めます。
式(1)のなかにあるτは、
$$せん断応力τ=\frac{P}{A}$$
なので、式(1)を式変形すると、
$$G=\frac{τ}{γ}=\frac{P}{A}×\frac{1}{γ}$$
せん断ひずみγを求めるためにさらに式変形する。
$$G=\frac{P}{Aγ}$$
$$G×\frac{A}{P}=\frac{\cancel{P}}{\cancel{A}γ}×\frac{\cancel{A}}{\cancel{P}}$$
$$\frac{AG}{P}=\frac{1}{γ}$$
$$γ=\frac{P}{AG} ・・・(2)$$
式(2)を使ってせん断ひずみγを求めます。
$$γ=\frac{P}{AG}=\frac{20×10^3}{30×60×80×10^3}$$
$$=0.000139=1.39×10^{-4}$$
解:せん断ひずみγ 1.39×10-4
例題3
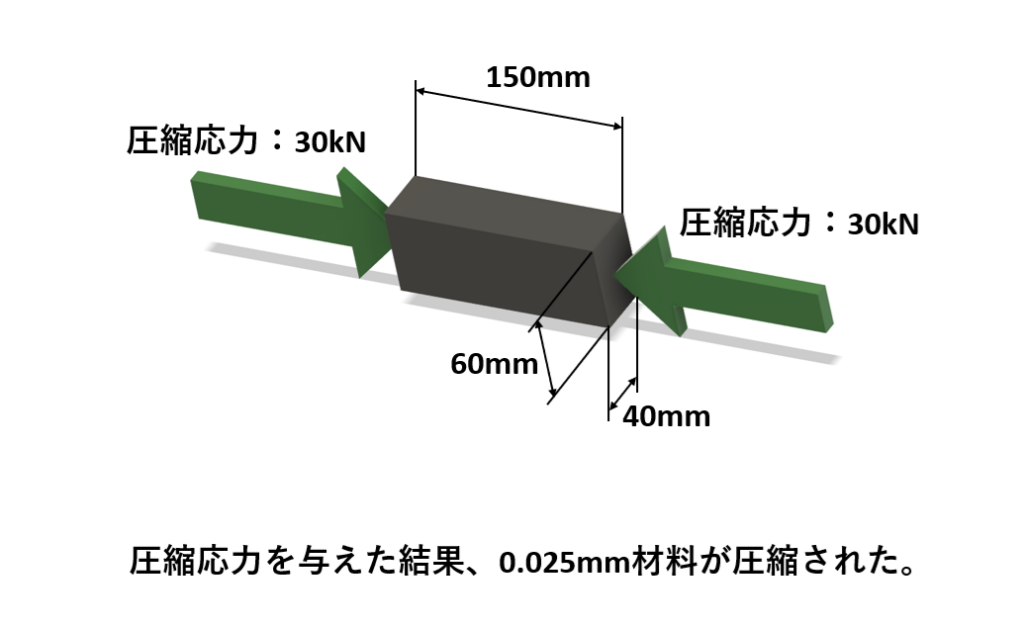
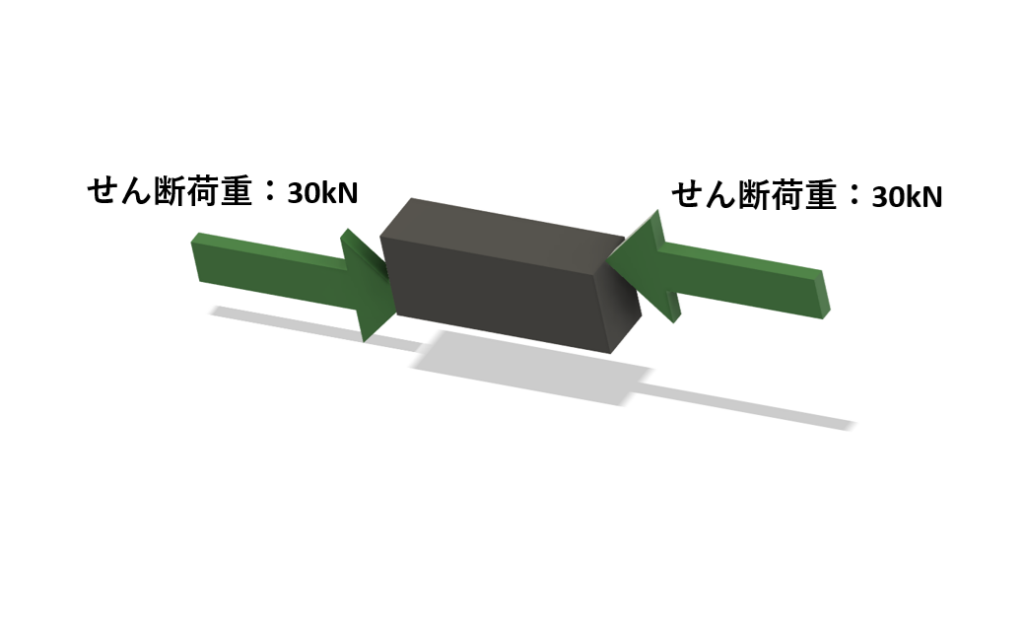
寸法が60mm×40mm×150mmの角材の各両端に30kNの圧縮荷重を与えた時、0.025mm材料が圧縮された。この圧縮荷重をせん断荷重に変更したときの材料に発生するせん断ひずみγを求めなさい。材料のポアソン比νは0.3とする。
ポイント
圧縮変形の条件から縦弾性係数Eを求めます。その横弾性係数とポアソン比の関係式を使って縦弾性係数Gを求め、最後にせん断ひずみγを導きます。
例題3の解答
縦弾性係数Eの式
$$E=\frac{Pl}{Aλ}$$
から縦弾性係数Eを求めます。
$$E=\frac{Pl}{Aλ}$$
$$=\frac{30×10^3×150}{60×40×0.025}=75,000MPa=7.50×10^4MPa$$
弾性係数とポアソン比の関係式を使って横弾性係数Gを求めたいので、G=~~~という形に式変形します。
$$E=2G(1+ν)$$
$$G=\frac{E}{2(1+ν)}$$
せん断ひずみの式
$$γ=\frac{P}{AG}$$
のGに先ほど式変形した式を代入します。すると、
$$γ=\frac{P}{AG}$$
$$=\frac{P}{A\frac{E}{2(1+ν)}}$$
$$=\frac{\frac{P}{1}}{\frac{AE}{2(1+ν)}}$$
$$=\frac{P×2(1+ν)}{A×E}$$
$$=\frac{30×10^3×2(1+0.3)}{60×40×7.50×10^4}$$
$$=0.0004333=4.33×10^{-4}$$
解:せん断ひずみγ 4.33×10-4
まとめ
ひずみとポアソン比は材料の挙動を理解するための鍵となる要素です。これらをマスターすることで、あなたの材料力学の知識は一層深まります。
これらの概念をしっかりと把握することで、より複雑な問題にも自信を持って取り組むことができるでしょう。次回もお楽しみに!
