「焼きばめ」と「冷やしばめ」は、金属部品を強固に結合するための方法です。
本記事では、これらの原理を簡単に説明し、基本的な数式で計算する方法をわかりやすく解説していきます。
焼きばめ(焼き嵌め)
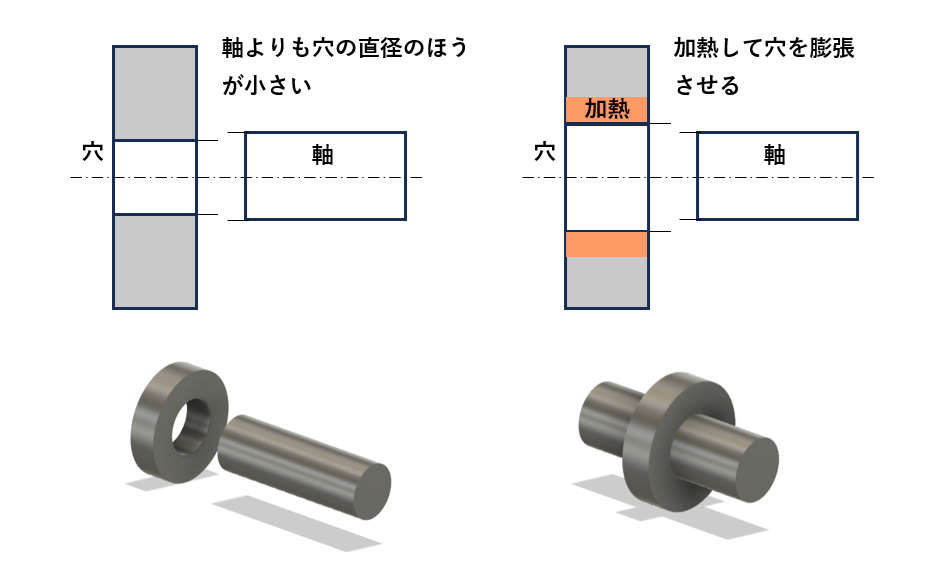
軸よりも直径の小さな穴を持つ輪を加熱し、熱によって膨張させます。膨張した穴に軸をはめ合わせ、常温まで放熱させると穴が収縮して、強固に結合することができます。
このような加工方法を焼きばめと呼びます。
主な用途としては、シャフトとギアのような回転部品で広く使用されている加工法です。
焼きばめのメリット・デメリット
焼きばめは一方の部品を高温で膨張させた状態で組み合わせ、冷却して接合力を得る方法です。
以下に、焼きばめの利点と欠点を詳しく説明します。
メリット
- 強力な接合力
焼きばめは、金属の膨張と収縮を利用して部品同士を固定するため、簡単な構造でも強い締結力を得ることができます。特に熱膨張率が高い材料であれば、より強固な接合が可能です。 - 構造のシンプルさ
ボルトやねじのような追加の締結部品が不要なため、部品の構造を簡素化できます。このため、コスト削減や製造工程の短縮にもつながります。 - 高い精度
焼きばめは、部品が冷却後に収縮してしっかり固定されるため、隙間のない接合が可能です。この特性から、振れやズレが許されない高精度な接合が必要な機械部品(例:例えば、マシニングセンタで搭載されている焼きばめホルダなど)でよく使用されます。 - 耐久性の向上
焼きばめによる接合は、部品の剛性を高め、振動や衝撃に対する耐性を向上させます。そのため、高速回転や高負荷がかかる環境でも安定した性能を発揮します。 - 良好なメンテナンス性
焼きばめホルダのように部品の構成がシンプルである場合、分解・清掃が容易で、メンテナンスがしやすいという利点があります。
デメリット
- 温度管理の難しさ
焼きばめは、高温に加熱する工程が必要です。そのため、加熱時の温度管理を適切に行わないと、部品に過剰な熱応力がかかり、材料が変形や損傷を受けるリスクがあります。 - 材料の制約
使用する材料の熱膨張率が低い場合や、熱に弱い材料の場合、焼きばめが適用できないことがあります。これにより、材料選定の幅が制限される場合があります。 - 専門的な設備が必要
焼きばめには、部品を均一に加熱するための専用の加熱装置や炉が必要です。また、適切な冷却工程も必要になるため、設備投資が必要となります。 - 取り外しが困難
焼きばめによって固定された部品は、接合力が強力であるがゆえに、後で分解するのが非常に難しい場合があります。特に、修理や部品交換が頻繁に行われる場合には不向きです。 - 作業の手間
部品を高温で加熱し、すぐに組み立てて冷却する必要があるため、作業時間が制約されることがあります。また、安全対策が必要になる点も手間となります。
焼きばめは、強力な接合力や高い精度が求められる場面で非常に有効な方法ですが、温度管理や設備の準備が必要であることから、デメリットも存在します。この技術を効果的に活用するためには、部品の材料や形状、作業環境を考慮し、適切に設計・計画することが必要です。
冷やしばめ(冷やし嵌め)
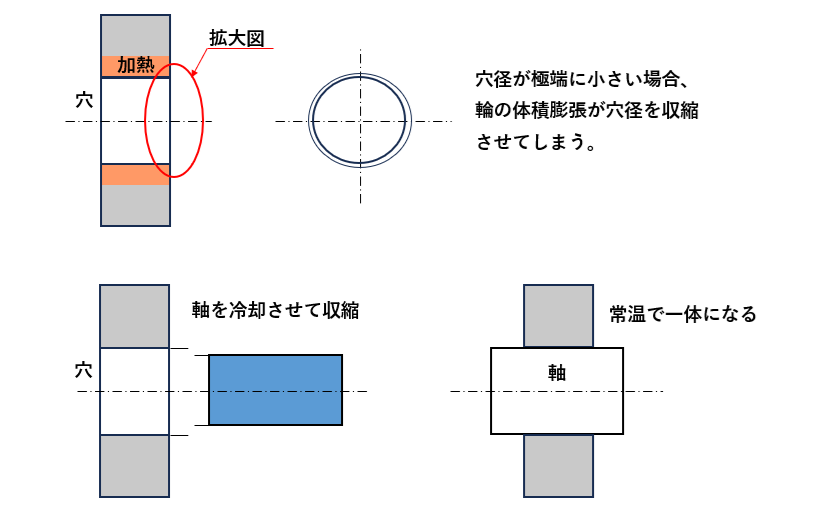
穴径が極端に小さい輪を加熱すると輪の体積膨張が穴径を収縮させ、はめ合わせができない場合があります。
このような場合、軸のほうを冷却して収縮させた軸と穴をはめ合わせることによって、軸が常温に戻った時穴と軸が一体になります。
このような加工方法を冷やしばめとよびます。
冷やしばめのメリット・デメリット
冷やしばめは金属部品を冷却して収縮させた状態で組み合わせ、常温に戻る過程で膨張して固定する接合技術です。
この方法は熱を加える必要がないため、焼きばめとは異なる特性を持ちます。以下に、冷やしばめの利点と欠点を詳しく解説します。
メリット
- 熱の影響を抑えられる
冷やしばめは部品を冷却する方法のため、焼きばめのように高温で材料に熱応力を与えるリスクがありません。そのため、熱に弱い材料や熱処理された部品にも適用しやすいのが利点です。 - 部品の寸法精度を保ちやすい
冷却による収縮は比較的安定しているため、組み立て後の寸法変化が最小限に抑えられます。これにより、精密な接合が求められる場面でも効果的に利用できます。 - 均一な冷却が可能
液体窒素やドライアイスを利用して冷却することで、部品全体を均一に冷却できます。これにより、部品が均一に収縮し、高い接合精度が得られます。 - 火災や酸化のリスクが低い
冷却工程のみで行うため、加熱に伴う火災リスクや金属表面の酸化を防ぐことができます。この点から、環境的にも安全性が高い方法と言えます。 - 取り外しが比較的容易
焼きばめに比べ、冷却による接合は加熱して膨張させれば取り外しが可能な場合が多いため、メンテナンス性が良いことがあります。
デメリット
- 冷却剤の取り扱いが必要
冷やしばめには液体窒素やドライアイスといった冷却剤を使用するため、それらを安全に取り扱うための知識や設備が必要です。また、これらの材料を適切に管理するコストが発生します。 - 作業環境の制約
冷却工程は低温環境を必要とするため、寒冷地や低温に弱い作業現場では取り扱いが難しい場合があります。また、冷却剤の蒸発や低温による周辺への影響も考慮する必要があります。 - 収縮の限界
冷却による収縮は、材料の熱膨張率と冷却温度の差に依存します。熱膨張率が小さい材料では、得られる締結力が制限される場合があります。 - 冷却材の影響
極低温による冷却は、金属材料の靭性を低下させることがあります。一部の材料では、冷却後に脆くなるリスクがあるため、注意が必要です。 - 適用可能な部品サイズの制限
大型部品や形状が複雑な部品では、均一に冷却するのが難しい場合があります。特に、部品全体を冷却剤に浸す必要がある場合、冷却設備の大きさや能力に依存します。
冷やしばめは、熱の影響を抑えながら高精度な接合が可能な方法であり、特に熱に弱い部品や高精度が求められる場面で有効です。ただし、冷却材の取り扱いや低温環境への対応が必要となるため、設備や作業環境が制約となる場合があります。
焼きばめとvs冷やしばめどっちが強固なのか?
結論から言うと、焼きばめと冷やしばめのどちらが強固に結合できるかは主に使用する材料や加工条件に依存するため、一概にこっちの方法だと強度があるからいいとは言い切れません。
結合させる部品の材質や形状、さらには作業環境や使用目的を考慮して選択することが重要なのです。
ですが、どっちの加工法を取るかの判断基準はあります。
焼きばめと冷やしばめは温度差が大きければ大きいほど締結力が強まるため、材料の熱膨張率や加工可能な温度差を考慮するといいです。
一般的に、焼きばめのほうが温度差が大きくなる傾向があり、強固な結合が可能になるケースが多いです。
そして冷やしばめは焼きばめと比べて熱による影響が少なく、このことから精密な部品や熱に弱い材料に向いている場合があります。
設計条件や使用する材料によって適切な方法を選びましょう。
材料力学での焼きばめ・冷やしばめの求め方
熱による金属の変形を利用して軸状部品とリング状部品を組み付ける加工法は、金属材料の熱膨張や収縮の特性を活用した接合技術です。
特にリング状の部品に注目すると、その構造が薄肉円筒として扱える場合があります。
焼きばめ・冷やしばめの接合時の応力は、フープ応力(周方向応力)の式を使うことによって計算できます。
フープ応力の式は、
$$フープ応力σ_{r}=\frac{pD}{2t}$$
となります。
フープ応力の内容や公式については、下記の記事をご覧いただければ参考になるかと思います。

計算問題
例題1
内径60mm、厚さ5mmの中空軸に、段付丸棒をはめ合わせたい。この時の軸のはめ合わせ部分の直径と、焼きばめ後の中空軸と段付きのシャフトの接合面に発生する圧力を求めなさい。中空軸の縦弾性係数は206GPa、許容引張応力は50MPaとする。

ポイント
・許容引張応力は、中空軸の内径がDになるときの応力と考えます。
・2つの部品の組付け後の圧力は、薄肉円筒のフープ応力の式を適用して計算する。薄肉円筒のフープ応力は、
$$フープ応力σ_{a}=\frac{pD}{2t}$$
を使います。
・中空軸の内径をd、dの膨張量をδとします。
例題1の解答
中空軸の膨張量はδ=D-dという式から考えていき、そのためにまずは横ひずみの関係式を導出していきます。横ひずみの式は、
$$ε’=\frac{δ}{d} ・・・(1)$$
となり、縦弾性係数Eの式は、
$$E=\frac{σ}{ε}$$
である。この式をεについて求める形にすると、
$$ε=\frac{σ}{E} ・・・(2)$$
となる。式(1)と式(2)を連立させると、
$$ε’=\frac{δ}{d}=\frac{σ}{E} ・・・(3)$$
となる。ここで、δ=D-dを式(3)に代入すると、
$$ε’=\frac{δ}{d}=\frac{σ}{E}$$
$$\frac{D-d}{d}=\frac{σ}{E}$$
$$\frac{D}{d}-1=\frac{σ}{E}$$
が得られます。さらに式を整理すると、
$$\frac{D}{d}-1=\frac{σ}{E}$$
$$\frac{D}{d}=\frac{σ}{E}+1$$
$$\frac{D}{d}=\frac{σ+E}{E}$$
$$D=\frac{d(σ+E)}{E} ・・・(4)$$
が得られます。式(4)にそれぞれの数値を代入します。
$$D=\frac{d(σ+E)}{E}$$
$$=\frac{60×(50+206×10^3)}{206×10^3}$$
$$=60.014563・・・=60.01mm$$
接合面の内圧は内圧を受ける薄肉円筒のフープ応力から求められるので、
$$フープ応力σ_{a}=\frac{pD}{2t}$$
$$p=\frac{2tσ_{a}}{D}$$
$$=\frac{2×5×50}{60.01}$$
$$=8.33MPa$$
解:はめ合わせ部分の直径 60.01mm、接合面の圧力 8.33MPa
まとめ
今回は焼きばめ・冷やしばめの内容と計算方法をご紹介しました。
このような内容でも材料力学の知識があれば、案外簡単に解けるんだなというのが体感できたかと思います。
今後も、工学に役立つ知識やテクニックをわかりやすくお伝えしていきますので、引き続きお楽しみいただければ幸いです。
