建築や構造設計で重要な『はり』について、その基本的な種類や反力の求め方をわかりやすく解説します。
本記事では、はりの種類と反力の求め方について解説しています。
はりの問題は最終的な本題に到達するまでに解決しなければならない、いくつかの計算ステップがあります。
具体的な計算方法についても記載していますので、最後まで御覧いただければなと思います。
梁(はり)の種類
荷重を受けるはりを支える方法は、次の3つに分類されます。
両端支持梁(単純支持梁)
両端支持梁(単純支持梁)とは、両端が支えられているはりのことです。建築や構造設計でよく登場する基本的なはりの種類の一つです。
両端支持梁の特徴
両端を固定や可動の支点で支えることで、荷重を受け止めます。両端で支えられている橋の状態をイメージするとわかりやすいです。
そして、中央や支点間に荷重がかかるという点も両端支持梁ならではの特徴で、支えられた両端の間に外力(荷重)が作用すると、はりはたわみ(曲がり)ます。
ちなみに、両端支持はりは材料力学のはり問題を学ぶ上で最も基本的な構造モデルとなるので、せん断力図や曲げモーメント図を描く練習にもよく使われています。
両端支持梁の物理的な挙動
両端支持梁に荷重がかかると、せん断力や曲げモーメントが発生します。
これによりはりはたわみますが、両端で支えられているためはり全体は安定しています。
片持ち梁
片持ち梁とは片方の端だけが固定され、もう片方が自由になっているはりのことです。建築や構造物で使われるはりの基本的な種類の一つで、片側だけで支えるという特徴があります。
片持ち梁の特徴
はりの一方の端が壁や柱にがっちり固定されており、動かないようになっています。もう片方の端は支えがなく自由な状態です。
荷重は主に自由端にかかることが多く、その力によってはりは曲げられたりたわんだりします。
片持ち梁の物理的な挙動
荷重がかかると、固定端にせん断力と曲げモーメントが集中します。これにより、固定端には反力とモーメントが発生します。
また、自由端に荷重がかかると、はりは撓る(しなる)ように変形します。
両端固定梁
両端固定梁とは、はりの両端がしっかり固定されている構造のことです。両端が動かないように固定されているため、他のはりに比べて剛性が高くたわみが発生しにくいのが特徴です。
両端固定梁の特徴
両端が壁や柱などにしっかりと固定されていることから、回転も移動もできない状態となっています。
そして、荷重がかかってもはり全体がたわみにくくなっており、曲げモーメントは両端に集中します。
これにより、他のはりよりも効率的に荷重を分散させることができます(剛性が高い)。
両端固定梁の物理的な挙動
両端が固定されているため、荷重がかかると両端に反力と曲げモーメントが発生します。
そして、他の支持形式(例えば両端支持はり)と比べて荷重によるたわみが大幅に抑えられ、中央部分のたわみが少ないことが特徴です。
両端固定梁に荷重がかかるとはり全体にわたって曲げモーメントが発生しますが、特に両端に大きなモーメントが集中します。
それぞれの支持形式をまとめるとこのようになります。
片持ち梁：一端だけが固定されており、もう片方は自由。
両端支持梁：両端が支点で支えられているが、回転は自由。
両端固定梁：両端が剛固定されており、回転も移動もできない。
荷重の種類
はりの問題における荷重には次のような種類があります。
集中荷重 (Point Load)
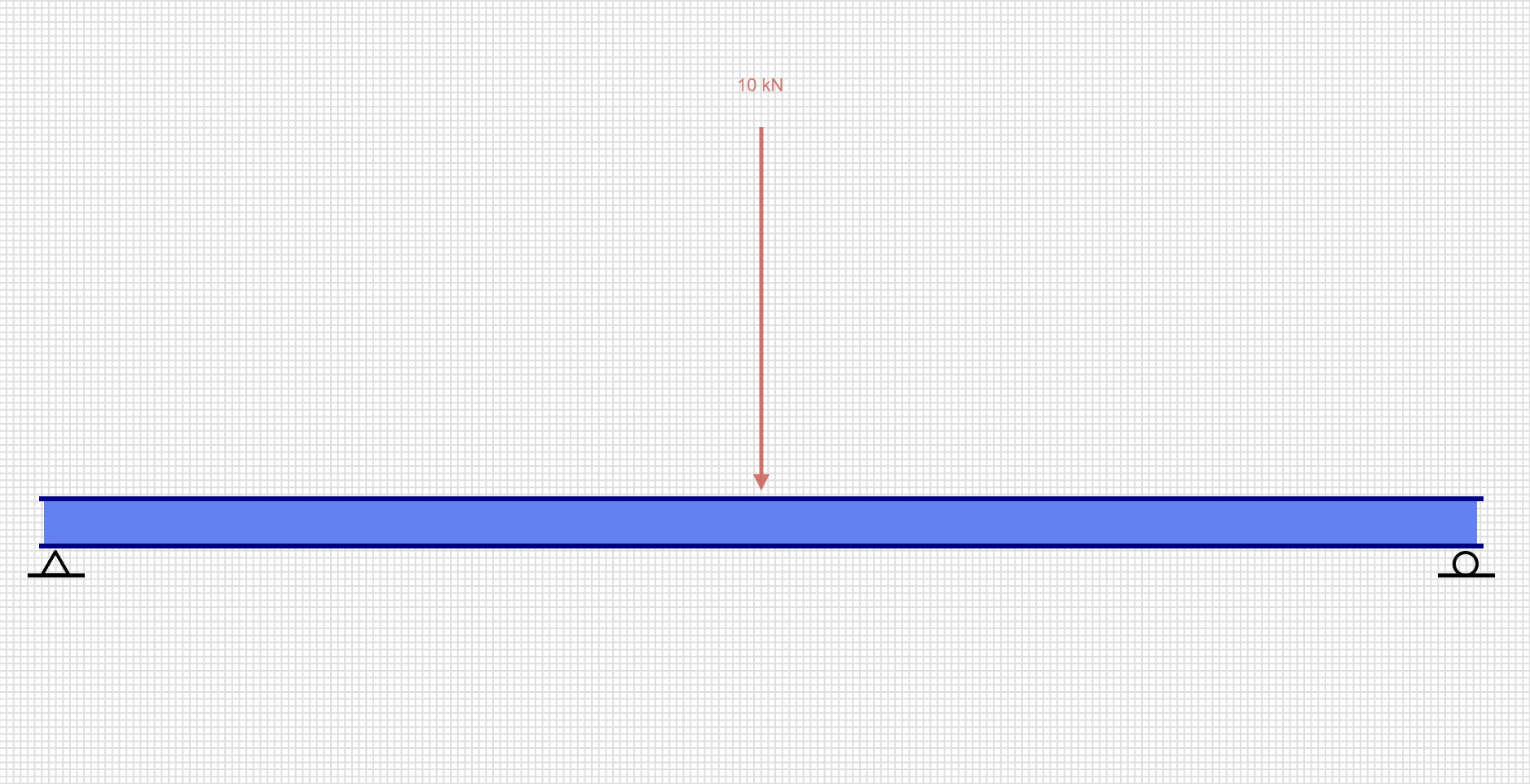
荷重が一点に集中して作用するものを集中荷重といいます。荷重が特定の一点に作用するため、簡単に計算できるのが特徴です。
集中荷重は通常、ニュートン(N)やキロニュートン(kN)で表されます。
集中荷重の具体例
- 本などの机の上に置かれた1つの重たい物体。
- 橋の上を走る車両が特定の箇所に荷重を与える場合。
分布荷重(Distributed Load)
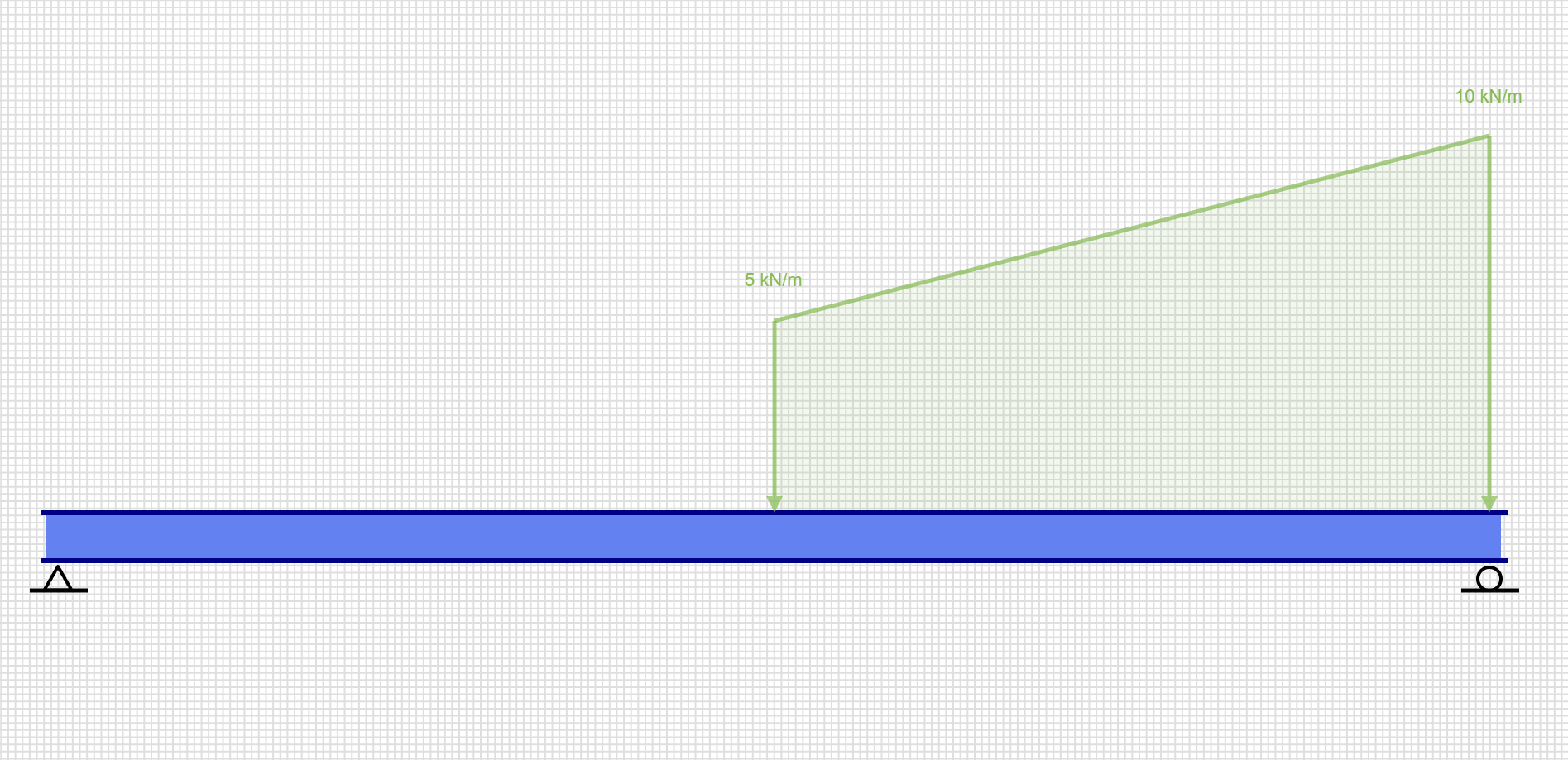
荷重が広がって分布し、複数の点にわたって作用するものを分布荷重といいます。ある範囲内で不規則または規則的に分布する荷重のことを指します。
分布荷重の力の単位はN/m(またはkN/m)で表されます。
分布荷重の具体例
- 長い本棚に様々な重さを持つ本が収納されている。
- 橋全体にかかる歩行者や車両の重量。
等分布荷重 (Uniformly Distributed Load, UDL)
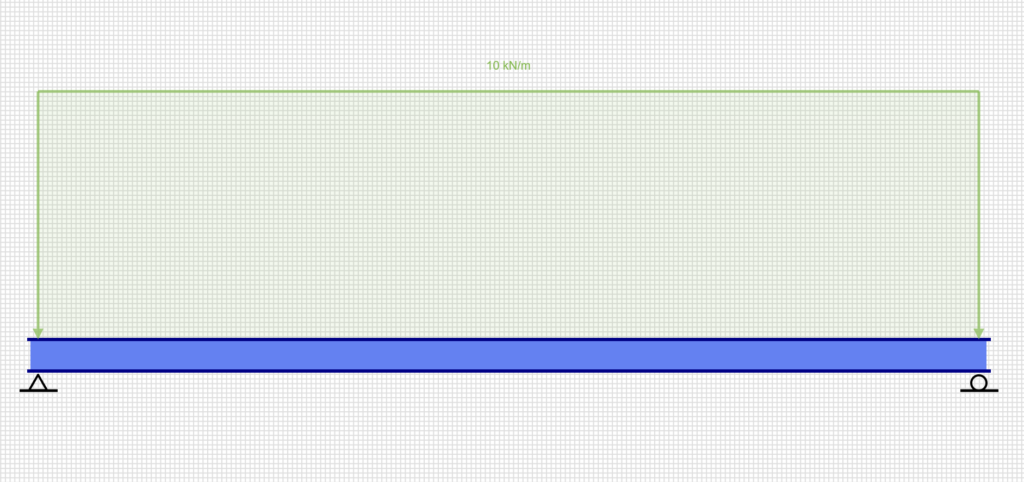
荷重が広がって分布し、複数の点にわたって均等に作用するものを分布荷重といいます。
長さあたりの力(力の単位)は分布荷重と同じくN/m(またはkN/m)で表されます。
等分布荷重の具体例
- 長い棚にびっしり詰まった同じ重さの本。
- 屋根に均等に降り積もった雪。
支点の種類
支点には、力やモーメントをどのように伝えるのかによっていくつかの種類があります。
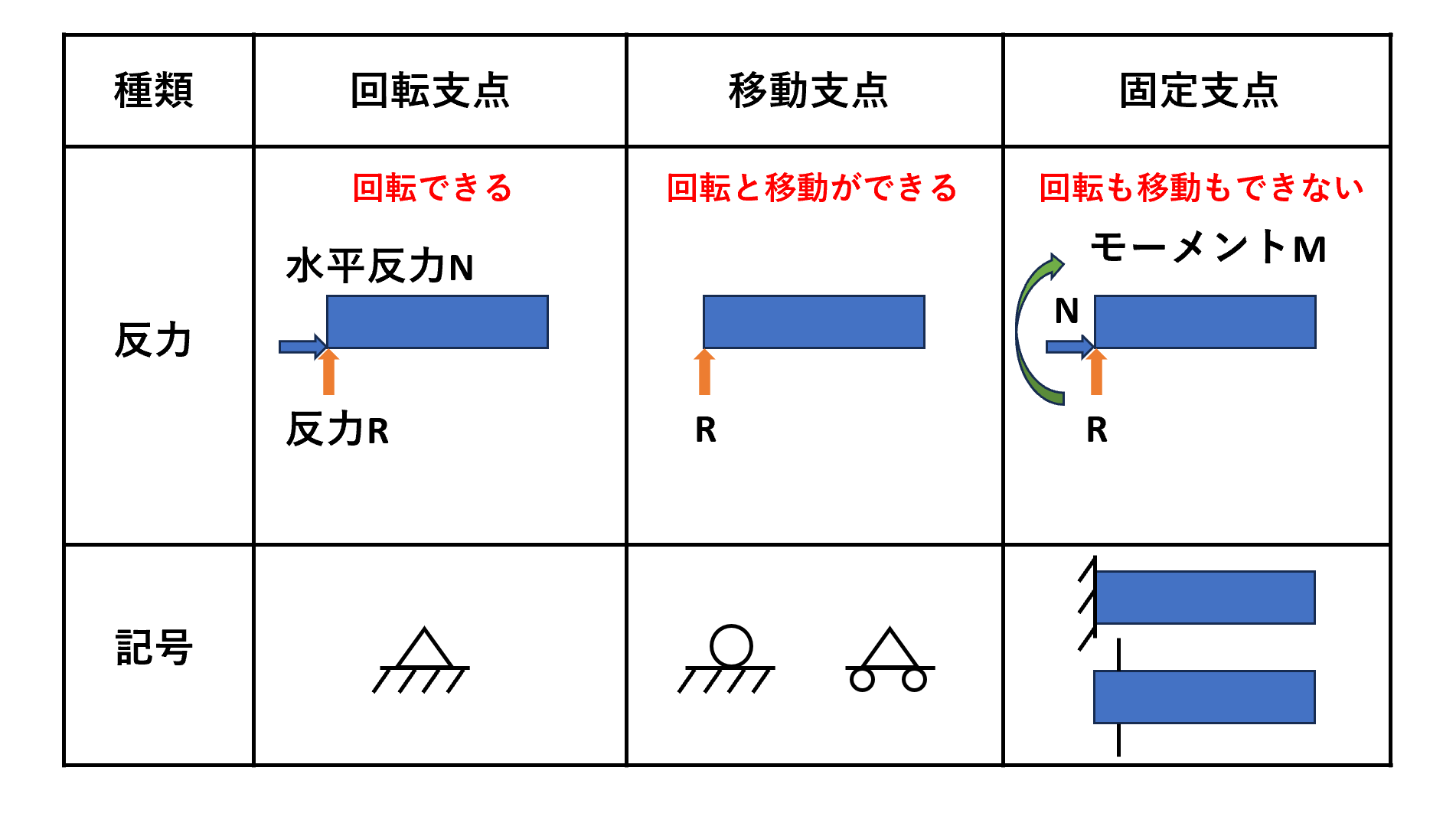
回転支点(ピン支点・ヒンジ支点)
回転支点は自由に回転するが、水平・鉛直方向は固定された状態をいいます。
そのため、水平方向と鉛直方向の2方向に反力を発生させますが、回転は許容します。
用途
橋梁や建築物の柱などで使われることが多い支点です。
移動支点(ローラー支点・可動支点)
水平方向は自由に移動し自由に回転できますが、鉛直方向は固定された(移動できない)支点のことをいいます。
用途
大型構造物や橋梁の一部で、温度変化や振動を考慮する必要がある箇所に用いられる。
固定支点
水平および鉛直方向は固定され、かつ回転もできない支点を固定支点といいます。
固定支点は水平方向、鉛直方向、回転方向すべてに反力（またはモーメント）を発生させます。
用途
橋梁の基礎部分や壁と梁の接合部分で使用される。
はりの問題を解く際の重要なポイント
はりの問題は、求める事柄が多いため順を追って解いていくことが大切です。
ここでは計算問題に入る前に、前提知識としておさえておいたほうがいい内容をピックアップしています。効率よく問題を解くための基礎固めとして参考にしてください。
以下のポイントを意識することではりの問題に取り組む際の理解が深まり、計算ミスや抜け漏れを防ぐことができるかと思います。
静定はり
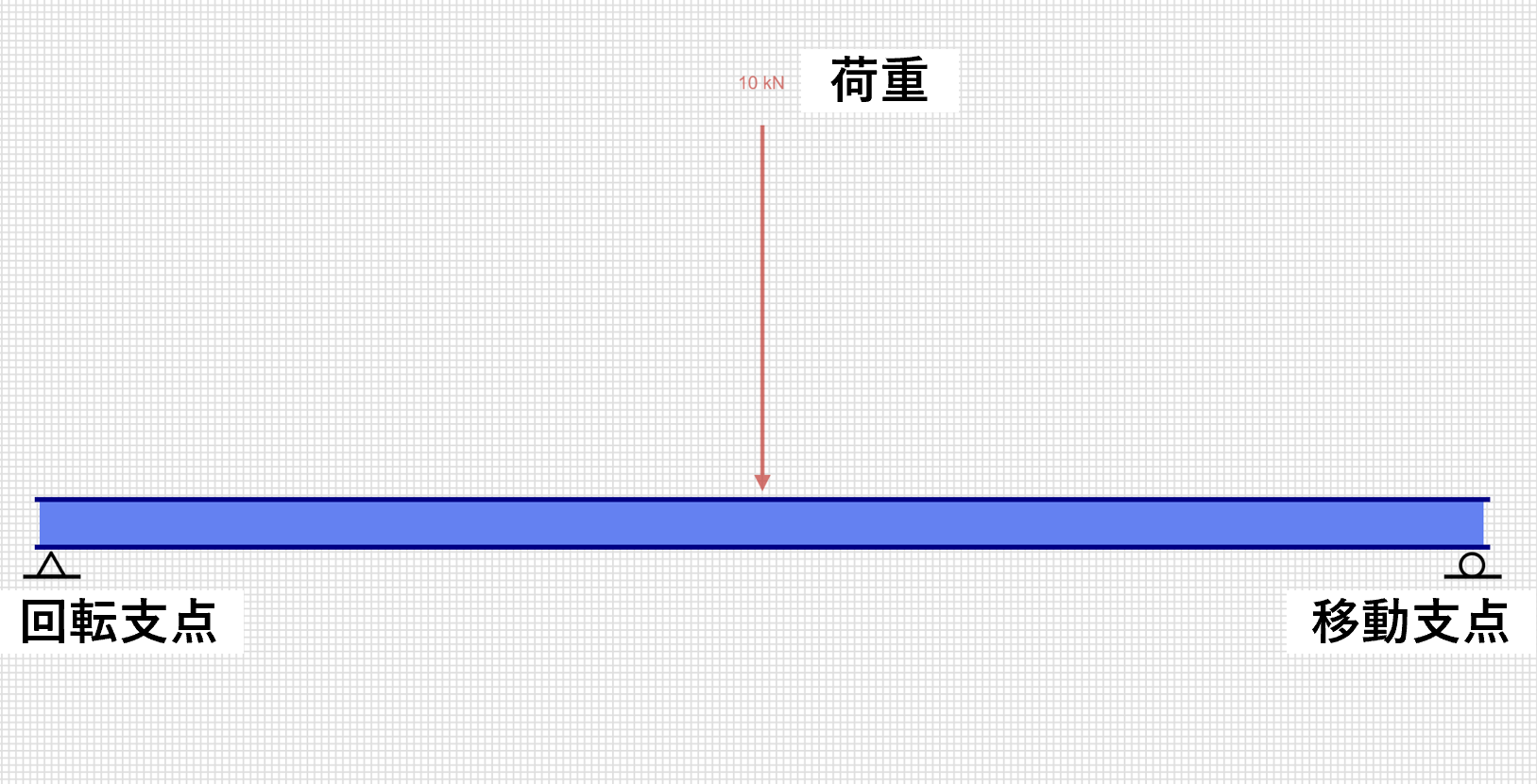
回転支点と移動支点で水平に支えた両端支持はりに、鉛直下向きに荷重が作用していた場合、はりは拘束されず自由に変形できるので、荷重がはりに与える影響だけを考えることができます。このような場合を静定はりといいます。
支点反力
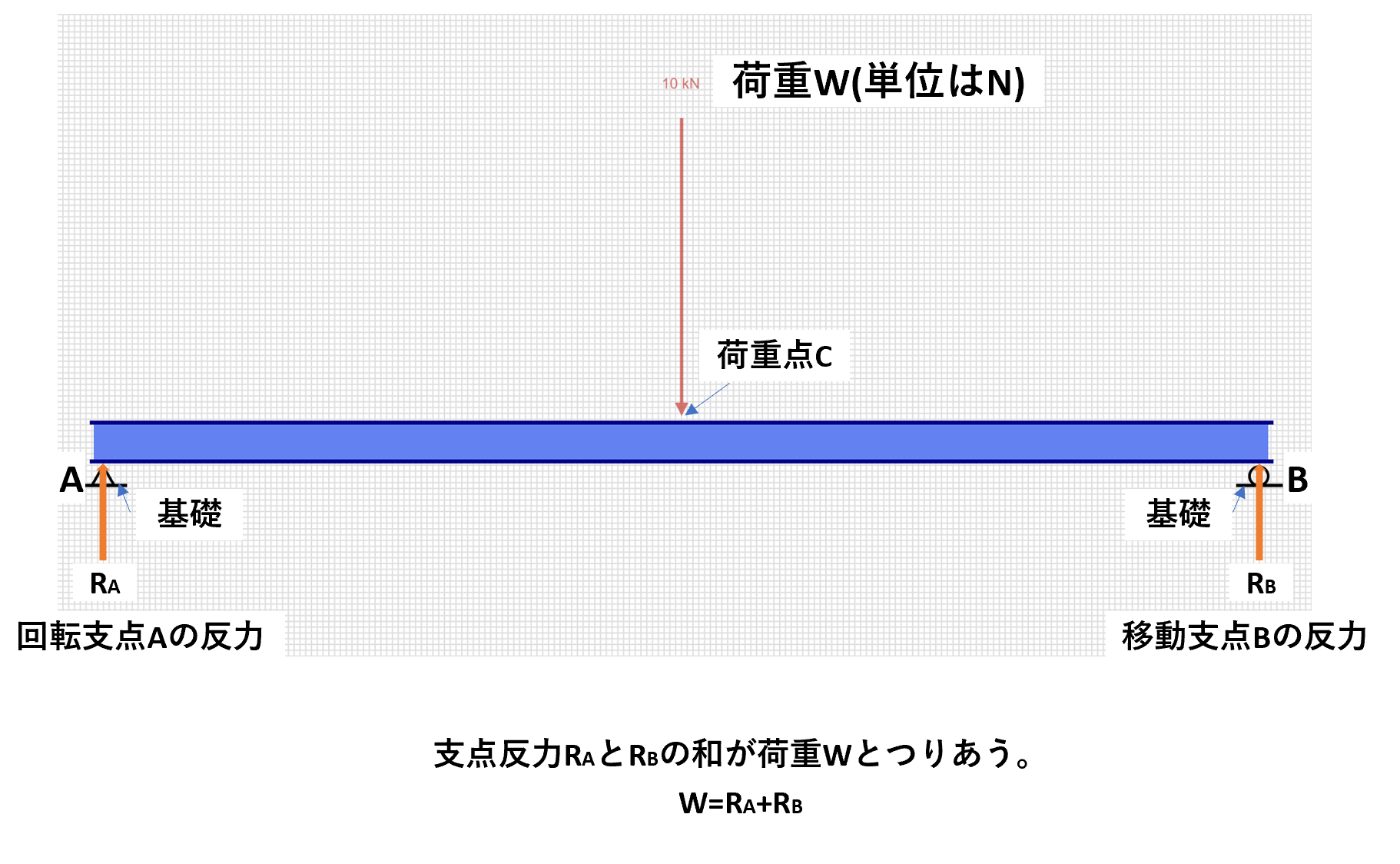
下図の両端支持はりの固定支点Aと移動支点Bでは、基礎によって支えられています。このはりに外力として荷重Wが作用すると、荷重は支点を介して２つの基礎で受け止めます。
基礎は荷重Wの反作用として、荷重の反対向き(鉛直上向き)の反力をはりに与えます。
この支点に生じる反力を支点反力と呼び、はりにとっては外力となります。
下図は支点反力RAと支点反力RBの和が荷重Ｗとつりあい、はりは静止している状態を表しています。
せん断力
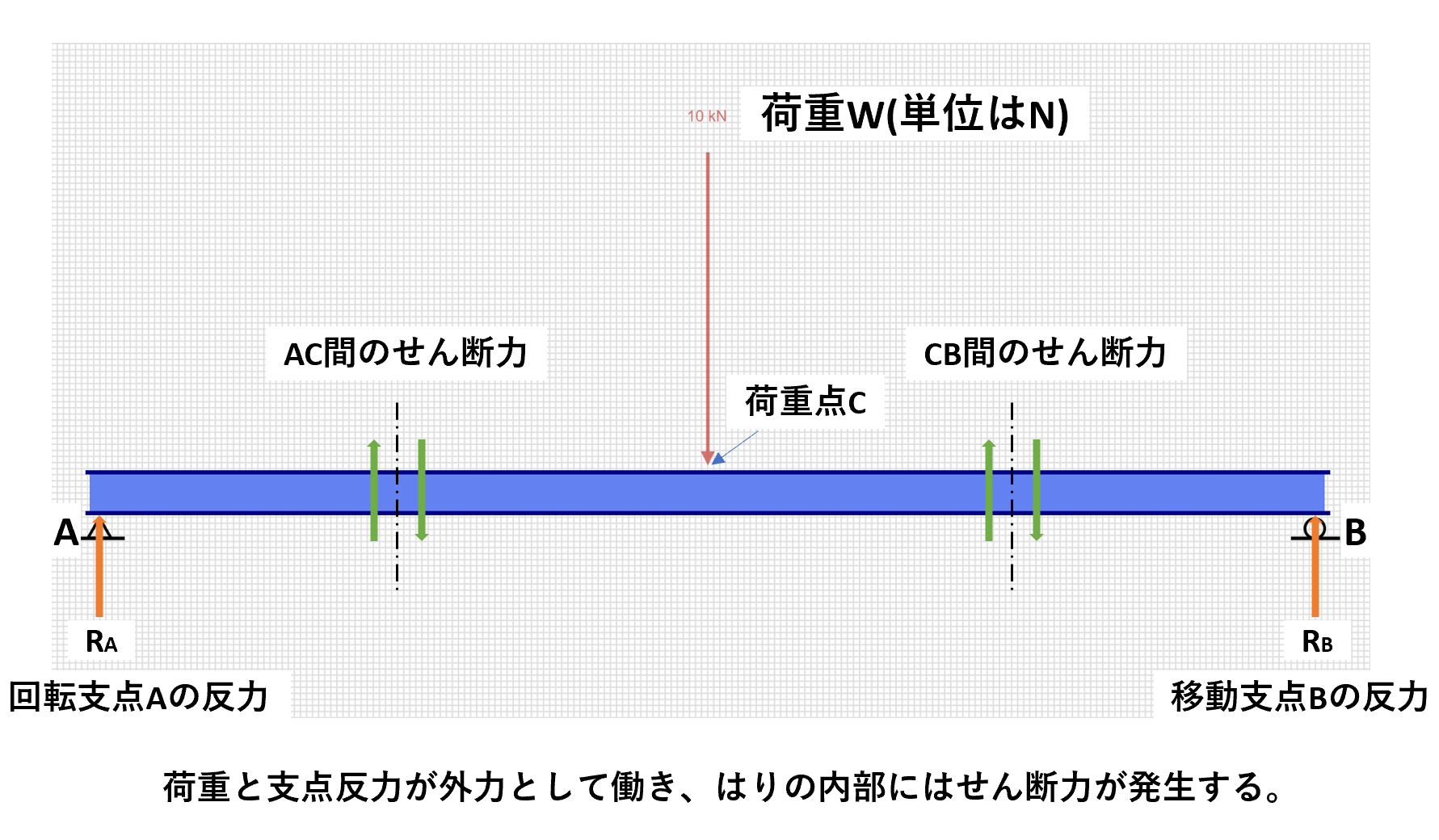
荷重や支点反力といった外力を受けて静止状態を保っているはりでは、仮想的な任意の断面を考えるとその断面の両側に等しい大きさで反対方向の内力が働きます。
この内力は材料をせん断しようとする性質を持つため、はりの内部にはせん断力が発生します。
曲げモーメント
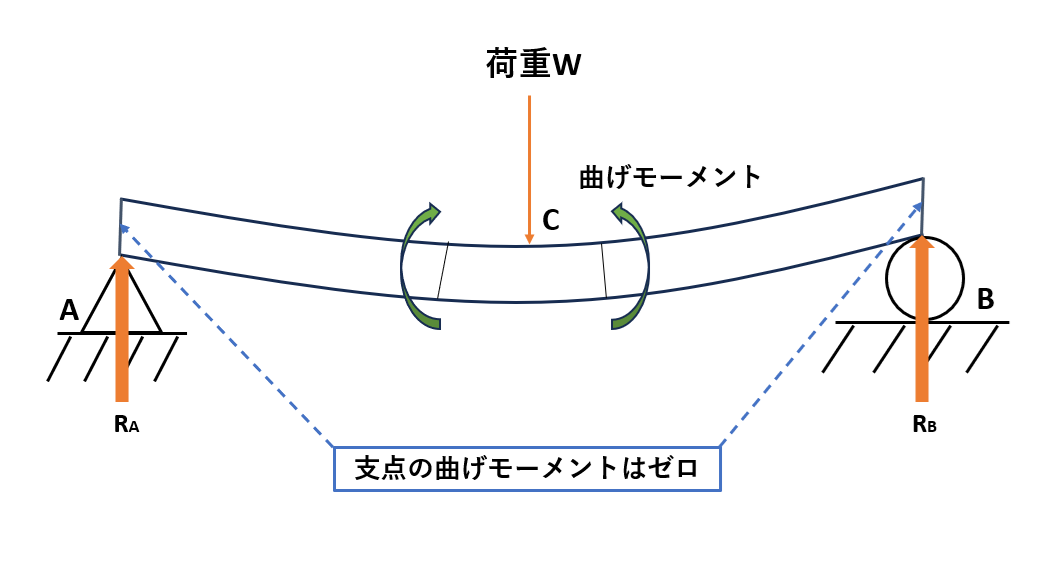
はりに作用する外力は、はりを回転させようとする力のモーメントを発生させます。下図のように荷重Wが発生していると、はりの内部ではすべての任意の仮想断面で反作用として逆向きのモーメントが発生しています。
はりの内部に生まれるモーメントは、はりが回転しないように静止させると同時にはりを曲げるようにして力が働きます。この力のことを曲げモーメントと呼びます。
はりの問題は支点反力から計算する
はりの問題は、支点反力を求めることから始まります。
この機会に力のつり合いと力のモーメントのつり合いに慣れていきましょう。
両端支持梁の支点反力について
支点反力を求めるために、最初に両端支持梁をの真ん中に集中荷重Wが作用している状態をイメージしてみてください。
この両端支持梁というのは梁問題を正確に解くための登竜門とも言える基本的なケースですので、まずはそこから考えてみたいと思います。
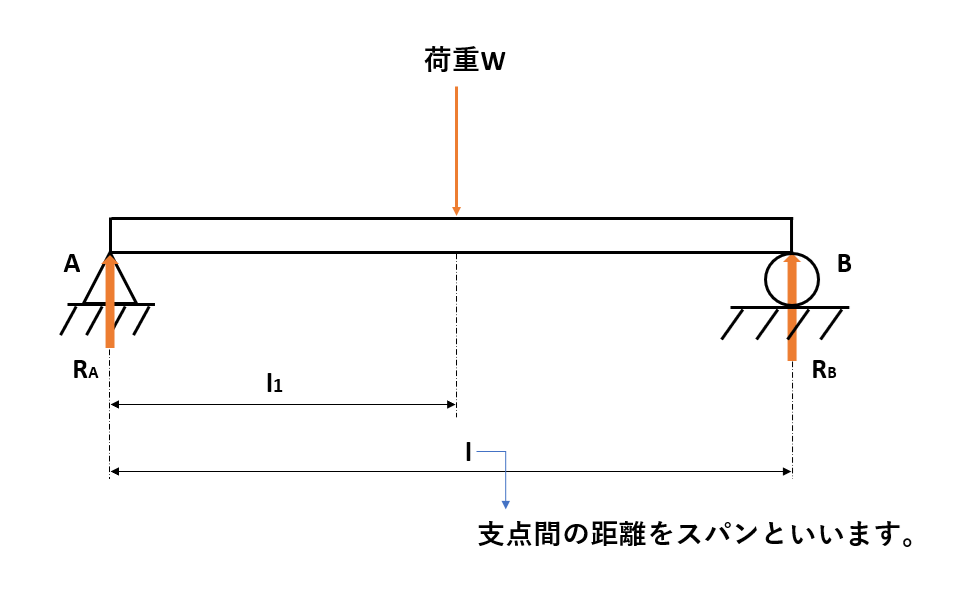
支点間の距離l(エル),支点Aから距離l1の点に集中荷重Ｗが作用する両端支持はりの支点反力RA、RBの関係は以下のようになります。
支点間の距離は別名スパンとも呼びます。
はりが静止するための条件
材料力学ではりが静止するための条件というのは以下のように定義づけられています。
力の総和がゼロ
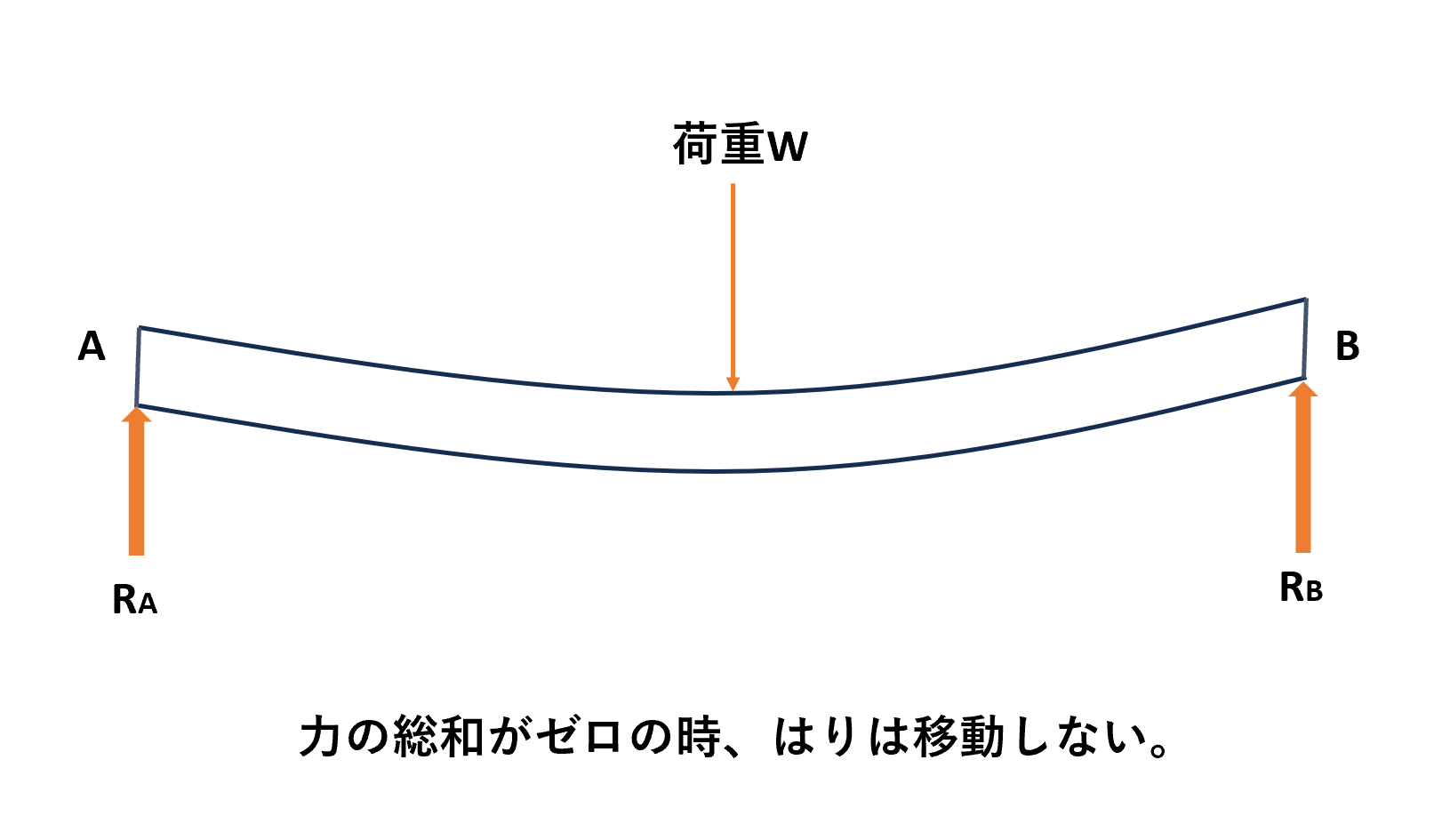
はりが静止している状態というのは、移動も回転もしない状態のことです。
そして、はりが移動しない条件というのは、はりに作用する鉛直下向きの荷重と、鉛直上向きの支点反力の合計がゼロになるということ、つまり力の総和がゼロということです。
例えば下図のような条件では、
$$荷重-支点反力R_{A}-支点反力R_{B}=0$$
$$荷重W=支点反力R_{A}+支点反力R_{B}$$
となります。
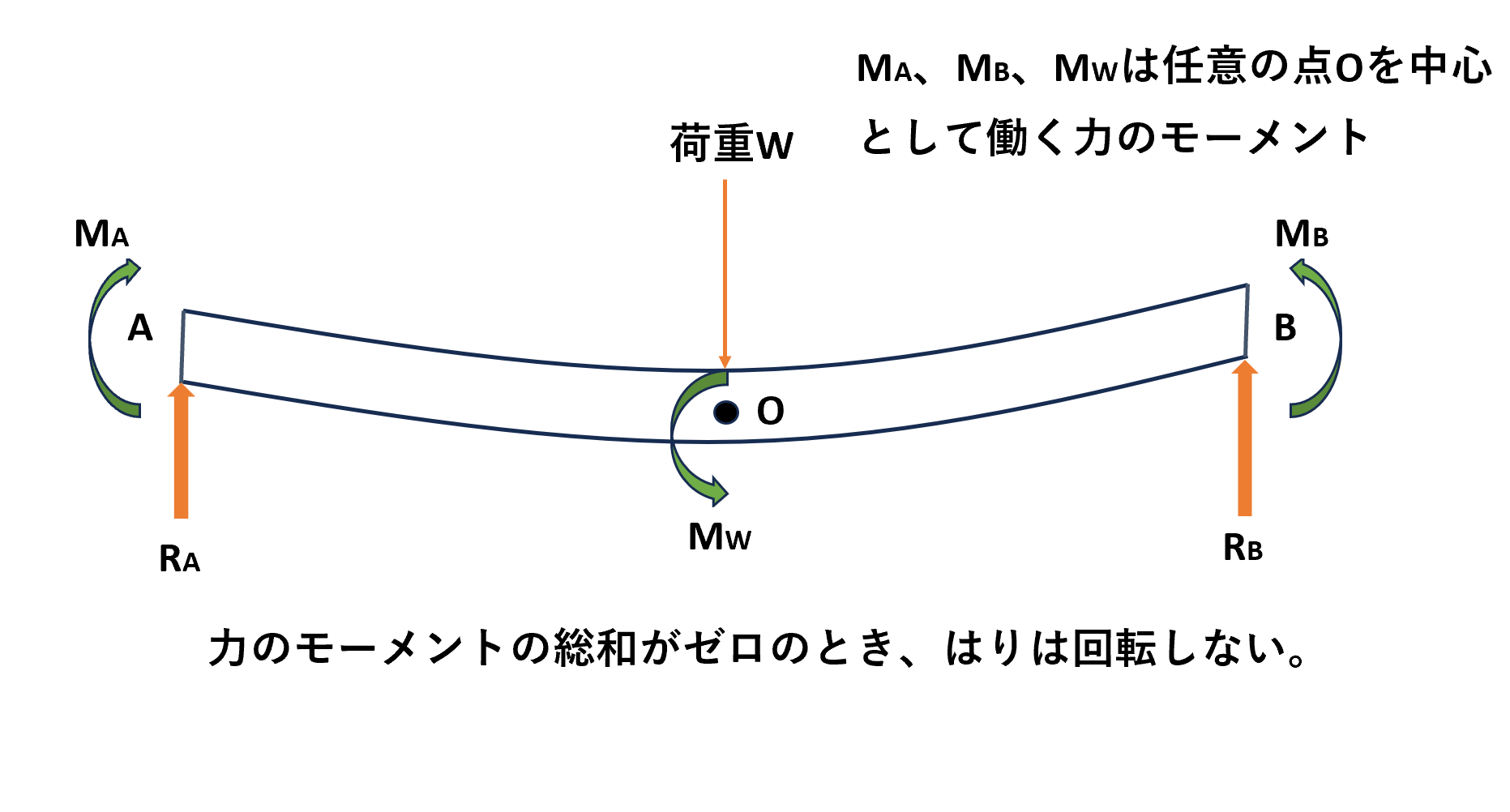
力のモーメントの総和がゼロ
荷重と支点反力は、はりを回転させようとする力のモーメントを発生させます。このことから、はりが回転しないということは、はりに働く力のモーメントの総和がゼロということになります。
支点反力の計算の方法
前項では力の総和がゼロ、力のモーメントの総和がゼロという２つの条件を記載しました。
その前提条件をもとに、ここでは２つの支点反力(RA、RB)を求めていきたいと思います。
計算するにあたって、力の方向は以下のように定義しています。
| 力の向き | 符号 |
| 下向きの力 | + |
| 上向きの力 | － |
| 反時計回りのモーメント | + |
| 時計回りのモーメント | － |
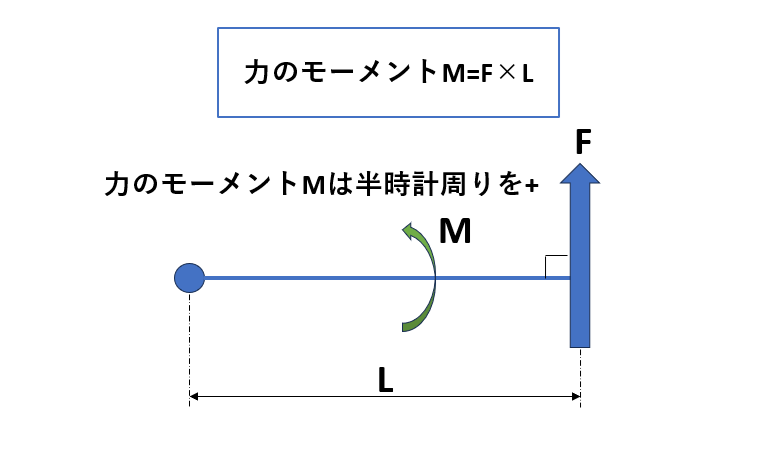
力のモーメントは、
$$モーメント(M)=腕の長さ(l)×力(荷重W，反力R)$$
から求めることができます。
そして、上記の表のように力の方向を定義した際、支点Aを基準とした力と力のモーメントは以下のようになります。
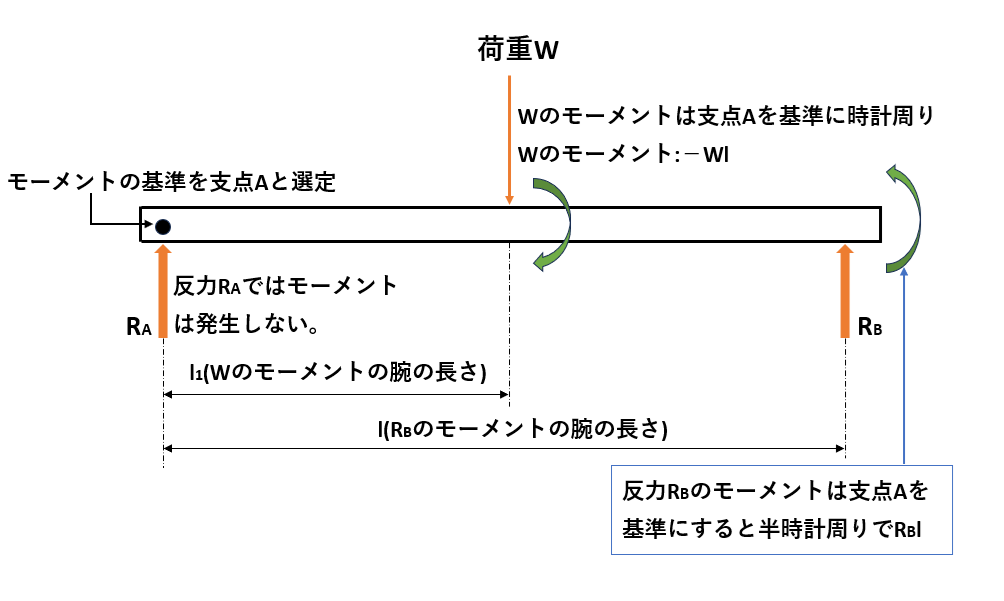
上の図をもとに、それぞれの重要ポイントを解説します。
まず、上向きの力と下向きの力を足すとゼロになるという式を立てます。下向きの荷重の力を+、上向きの支点反力の力を－としたので、
$$-R_{A}-R_{B}+W=0$$
$$R_{A}+R_{B}=W ・・・(1)$$
となります。
次に、支点Aを基準として力のモーメントの計算をしていきます。点Aを基準にすることにより、支点反力RAの腕の長さがゼロになり、モーメントの計算を１つ省くことができます。
$$R_{A}×0-W×l_{1}+R_{B}×l=0$$
$$-Wl_{1}+R_{B}l=0 ・・・(2)$$
ちなみにこの基準の取り方は任意の点で取ることができますので、ご自身の解く問題によって基準点を柔軟に選んでみてください。例えば、反力が働く支点や、複数の力が交差する点を基準とすることで、効率的にモーメントの計算が進められることが多いです。問題ごとに基準点を変えながら試行錯誤すると、モーメントの考え方に慣れるかと思います。
力のモーメントの総和がゼロという式(2)を式変形して、RBを求めます。
$$-Wl_{1}+R_{B}l=0 ・・・(2)$$
$$R_{B}l=Wl_{1}$$
$$R_{B}\cancel{l}×\frac{1}{\cancel{l}}=Wl_{1}×\frac{1}{l}$$
$$R_{B}=\frac{Wl}{l} ・・・(3)$$
最後に式(3)で導出した数値を式(1)に代入します。
$$R_{A}=W-R_{B}$$
まとめ
この記事を通では、はりの基本的な種類や反力の求め方を掲載しました。
実際の問題例や解答手順につきましては、別記事でもっと細かく記載しようと思います。
建築や構造設計の基礎を学びたい方、または復習したい方にとって今回の内容がお役に立てれば幸いです。