今回は材料力学の中でも少し計算が大変な熱を受ける組み合わせ部材の問題に挑戦してみましょう。
本記事では計算量が多くなる問題を取り上げますので、読んでいるだけではなく、ぜひ実際に紙に計算式を書きながら進めていってください。
問題を解くことで理解が深まること間違いなしです。それでは一緒に学びを深めていきましょう！
剛体壁に挟まれた材料における変形量の考え方
今回取り扱う内容はそれぞれ異なる２つ材質をもつ部材(ここでは銅パイプと鋼丸棒)が、常温から高温(もしくは低温)にさらされたときに発生する材料の伸び縮みに関する問題です。
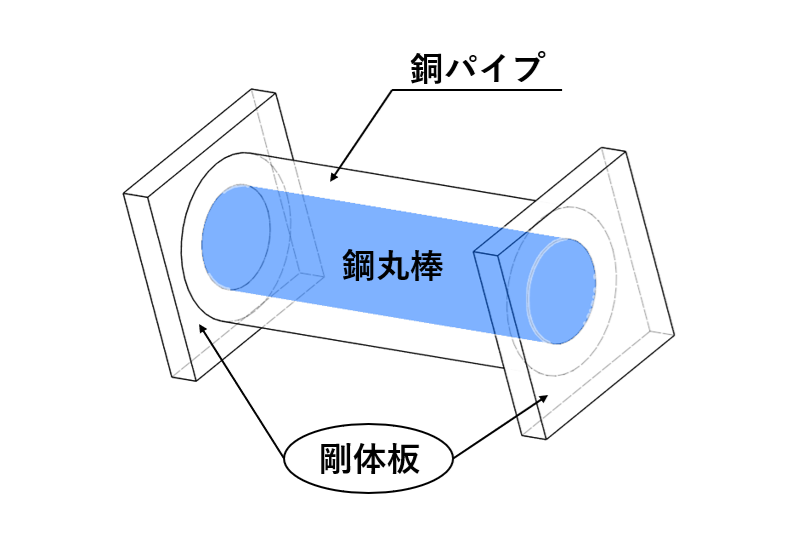
このような問題では、両者の変形量が等しいという条件に注目して、イコールの関係が成り立つような式を立てて計算していきます。
具体的には、以下のような内容が重要になってきます。
拘束条件のつり合い式を立てる
銅パイプと鋼丸棒は、その両端が剛体板で固定されているため、全体としての変形が一体的に制約されます。このため、両者の変形量は釣り合わなければなりません。
よってつり合いの式は、
$$λ(銅パイプの変形量)=λ(鋼丸棒の変形量)$$
というように表します。
自由変形量と拘束量を含んだ等式で表す
各部材にはそれぞれ温度上昇に伴う自由変形量（温度変化による自然な伸び）と、実際に拘束されているために生じる拘束量（変形が制限されて起こる応力による変形）が存在します。
これらを考慮すると、銅パイプの変形量と鋼丸棒の変形量は等しく、自由変形量と拘束量が存在する必要があります。
よって以下の等式で両者のひずみ量を表します。
$$λ_{1}+λ_{1}’=λ_{2}+λ_{2}’$$
λ1：銅パイプの自由変形量
λ1‘：銅パイプの拘束量
λ2：鋼丸棒の自由変形量
λ2‘：鋼丸棒の拘束量
変形が均一であることを表す
両者が一体となっているため、温度変化による変形は全体として均一に分配されます。
したがって、各部材の自由変形量と拘束量を足したものが等しくなります。
例えば、銅パイプではこのように表します。
$$λ=λ_{1}+λ_{1}’$$
λ：変形量の合計
λ1：銅パイプの自由変形量
λ1‘：銅パイプの拘束量
計算問題
例題１
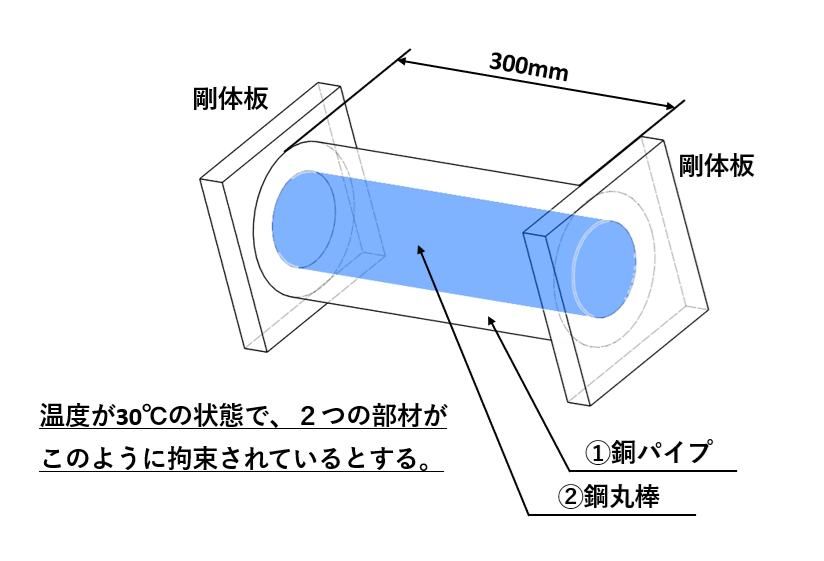
温度が30℃の状態で、①銅製のパイプと②鋼製の丸棒がそれぞれの両端を剛体板で固定され、全長300mmの部材を形成しています。この部材の温度が100℃に上昇したとき、①銅パイプと②鋼丸棒に発生する応力を求めてください。なお、各材料の特性は以下の通りです。
①銅パイプ：断面積550mm²、縦弾性係数100GPa、線膨張係数17.6×10⁻⁶
②鋼丸棒：断面積350mm²、縦弾性係数206GPa、線膨張係数11.5×10⁻⁶
今回の内容のキーポイント
温度変化によって拘束された銅パイプと鋼丸棒の変形量が等しいため、以下のポイントを押さえて両者の応力を計算していきます。
銅パイプと鋼丸棒は両端が剛体板で固定されています。温度変化による膨張や収縮が発生しても、これらの部材は互いに連結された状態なので変形量が等しくなります。両者の変形量は同じである、ということを説明できる式をたてましょう。
各部材の変形量は、温度変化によって生じる膨張（自由変形量）と、他の部材との拘束による変形（拘束変形量）の合計として表されます。自由変形量は材料が単独で温度変化に応じて変形できる量ですが、実際には剛体板によって制約を受けているため、拘束変形量も発生します。
このような組み合わせ部材では、銅パイプと鋼丸棒にかかる軸力の合計はゼロになります。これは静力学の原則に基づいており、外部からの力が働かず全体が静止している場合、内力のつりあいが成立するためです。例えば、温度変化によって銅パイプに引っ張られる力が発生するとすれば、鋼丸棒も同じ大きさで引っ張られる力を受けることになります。
そしてこの銅パイプと鋼丸棒にかかる軸力の合計はゼロになる、という等式を立てるには、応力の公式を変形して表します。
例題１の解答
①銅パイプの変形量
$$λ=銅パイプの自由変形量λ_{1}+拘束量λ_{1}’$$
②鋼丸棒の変形量
$$λ=鋼丸棒の自由変形量λ_{2}+拘束量λ_{2}’$$
①銅パイプの変形量と②鋼丸棒の変形量が等しいため、式で表すと以下のようになります。
$$λ_{1}+λ_{1}’=λ_{2}+λ_{2}’ ・・・(1)$$
①銅パイプの変形量と②鋼丸棒の自由変形量を求めます。式は、
$$変形量λ = αlΔt=αl$$
を使い、銅パイプと鋼丸棒それぞれの式を用意します。
$$①銅パイプの変形量λ_{1} = α_{1}lΔt ・・・(2)$$
$$②鋼丸棒の変形量λ_{2} = α_{2}lΔt ・・・(3)$$
縦弾性係数Eの式を式変形します。
$$E＝\frac{σ}{ε}$$
$$ε＝\frac{σ}{E}$$
応力とひずみの関係から、それぞれの拘束量を求めます。
$$ε＝\frac{σ}{E}＝\frac{λ}{l}$$
$$λ＝\frac{σ}{E}l$$
$$①銅パイプの拘束量λ_{1}’=\frac{σ_{1}}{E_{1}}l ・・・(4)$$
$$②鋼丸棒の拘束量λ_{2}’=\frac{σ_{2}}{E_{2}}l ・・・(5)$$
熱応力を求めるために、式(1)に式(2)～式(5)までのλを代入していきます。
$$λ_{1}+λ_{1}’=λ_{2}+λ_{2}’$$
$$α_{1}\cancel{l}Δt+\frac{σ_{1}}{E_{1}}\cancel{l}=α_{2}\cancel{l}Δt+\frac{σ_{2}}{E_{2}}\cancel{l}$$
$$α_{1}Δt+\frac{σ_{1}}{E_{1}}=α_{2}Δt+\frac{σ_{2}}{E_{2}} ・・・(6)$$
応力の公式、
$$σ＝\frac{P}{A}$$
であり、これをPについて式変形すると、
$$P＝σA ・・・(7)$$
となる。式(7)を使って、①銅パイプの軸力と②鋼丸棒の軸力がつり合うことを説明する関係式を立てると、
$$σ_{1}A_{1}+σ_{2}A_{2}=0$$
となり、σ2についての式に式変形すると、
$$σ_{1}A_{1}+σ_{2}A_{2}=0$$
$$σ_{2}=-σ_{1}\frac{A_{1}}{A_{2}} ・・・(8)$$
を得ることができます。
式(8)を式(6)に代入してσ2を消去し、式を整理します。
$$α_{1}Δt+\frac{σ_{1}}{E_{1}}=α_{2}Δt+\frac{σ_{2}}{E_{2}}$$
$$α_{1}Δt+\frac{σ_{1}}{E_{1}}=α_{2}Δt-\frac{σ_{1}A_{1}}{E_{2}A_{2}}$$
$$\frac{σ_{1}}{E_{1}}+\frac{σ_{1}A_{1}}{E_{2}A_{2}}=α_{2}Δt-α_{1}Δt$$
さらに同類項を整理し、σ1についての式を導出していきます。(右辺も整理します。)
$$\frac{σ_{1}}{E_{1}}+\frac{σ_{1}A_{1}}{E_{2}A_{2}}=α_{2}Δt-α_{1}Δt$$
$$σ_{1}(\frac{1}{E_{1}}+\frac{A_{1}}{E_{2}A_{2}})=Δt(α_{2}-α_{1})$$
$$σ_{1}(\frac{E_{2}A_{2}}{E_{1}E_{2}A_{2}}+\frac{E_{1}A_{1}}{E_{1}E_{2}A_{2}})=Δt(α_{2}-α_{1})$$
$$σ_{1}(\frac{E_{2}A_{2}+E_{1}A_{1}}{E_{1}E_{2}A_{2}})=Δt(α_{2}-α_{1})$$
$$σ_{1}=\frac{E_{1}E_{2}A_{2}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}} ・・・(9)$$
式(9)を式(8)に代入して、今度はσ2を求めていきます。
$$σ_{2}=-σ_{1}\frac{A_{1}}{A_{2}}$$
$$σ_{2}=-\frac{E_{1}E_{2}\cancel{A_{2}}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}}\frac{A_{1}}{\cancel{A_{2}}}$$
$$=-\frac{E_{1}E_{2}A_{1}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}} ・・・(10)$$
式(9)と式(10)にそれぞれ数値を代入して、σ1、σ2を求めていきます。
$$σ_{1}=\frac{E_{1}E_{2}A_{2}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}} ・・・(9)$$
$$=\frac{100×10^3×206×10^3×350×(100-30)×(11.5-17.6)×10^{-6}}{206×10^3×350+100×10^3×550}$$
$$=-24.22MPa(符号がマイナスなので圧縮応力)$$
$$σ_{2}=-\frac{E_{1}E_{2}A_{1}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}} ・・・(10)$$
$$=-\frac{100×10^3×206×10^3×550×(100-30)(11.5-17.6)×10^{-6}}{206×10^3×350+100×10^3×550}$$
$$=38.06MPa$$
解
①銅パイプに生じる応力 圧縮応力24.22MPa
②鋼丸棒に生じる応力 引張応力38.06MPa
別解
σ1の計算結果を式(8)に代入すると、σ2を簡単に求めることができます。
$$σ_{2}=-σ_{1}\frac{A_{1}}{A_{2}}$$
$$=-\frac{-24.22×550}{350}$$
$$=38.06MPa$$
例題２
例題１の組み合わせ部材で全体の温度が-15℃になったとき、全体の変形量、①銅パイプと②鋼丸棒に生じる応力を求めなさい。
今回の内容のキーポイント
下記の流れで計算を進めていきます。
最初のステップは式(9)、
$$σ_{1}=\frac{E_{1}E_{2}A_{2}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}}$$
と式(8)、
$$σ_{2}=-σ_{1}\frac{A_{1}}{A_{2}}$$
を使ってσ1、σ2を求めていきます。
次に式(3)
$$λ_{1}’=\frac{σ_{1}}{E_{1}}l ・・・(4)$$
を使って、①銅パイプの拘束量λ1‘を求めます。その後、式(2)
$$①銅パイプの変形量λ_{1} = α_{1}lΔt$$
を使ってλ1を求めます。
①銅パイプの変形量
$$λ=銅パイプの自由変形量λ_{1}+拘束量λ_{1}’$$
最後に以下の式、
$$λ=λ_{1}+λ_{1}’$$
から全体の変形量を求めます。
例題２の解答
式(9)よりσ1を求めます。
$$σ_{1}=\frac{E_{1}E_{2}A_{2}Δt(α_{2}-α_{1})}{E_{2}A_{2}+E_{1}A_{1}}$$
$$=\frac{100×10^3×206×10^3×350×(-15-30)(11.5-17.6)×10^{-6}}{206×10^3×350+100×10^3×550}$$
$$=15.57MPa$$
式(8)よりσ2を求める。
$$σ_{2}=-σ_{1}\frac{A_{1}}{A_{2}}$$
$$=\frac{-15.57×550}{350}$$
$$=-24.46714・・・$$
$$=-24.47MPa(符号がマイナスなので圧縮応力)$$
式(4)を使って拘束量λ1‘を求めます。
$$①銅パイプの拘束量λ_{1}’=\frac{σ_{1}}{E_{1}}l$$
$$=\frac{15.57}{100×10^3}300$$
$$=0.04671mm=0.05mm$$
式(2)より自由変形量λ1を求めます。
$$①銅パイプの変形量λ_{1} = α_{1}lΔt$$
$$= 17.6×10^{-6}×300×(-15-30)$$
$$=-0.2376=-0.24mm$$
式(1)より、全体の変形量λを求める。
$$λ=λ_{1}+λ_{1}’=-0.24+0.05$$
$$=-0.19mm$$
解
銅パイプ：引張応力15.57MPa
鋼丸棒：圧縮応力24.47MPa
全体の変形量：0.19mm縮む。
今回の問題は静定問題です。
静定問題とは構造物が外力や温度変化によって変形する際に、変形や応力を求めるために必要な条件がすべて揃っている状態を指します。この場合、銅パイプと鋼丸棒は剛体板によって固定されており、それぞれの材料の特性（断面積、弾性係数、線膨張係数）がすべて与えられています。
温度変化によって発生する応力を求めるための必要なパラメータがすべて揃っているため、こういった内容の問題は静定問題として扱います。
まとめ
今回は少し計算量が多めの問題に取り組んでみました。
確かに計算は多いですが、材料にどんな力が働くのかを考えながら公式に沿って解いていけば、しっかりと答えを導き出すことができる問題かと思います。
おそらく大学の試験や建築士試験でもこのような似た問題が出題されるでしょうから、しっかりと理解しておきたいところですね。
何度も復習を重ねて、マスターしていきましょう。
今回の記事はここまで。
最後までお読みいただき、ありがとうございました！