段付き丸棒における引張荷重のシンプルな計算方法

「材料力学」と聞くと、なんだか難しそう…と思う方も多いのではないでしょうか？

でも、心配はいりません！今回は、初心者の方でも理解しやすい「段付き丸棒の引張荷重」について、シンプルに解説していきます。

材料力学の基礎からしっかり学び、自信を持って次のステップに進めるようサポートしますので、一緒に学んでいきましょう！

段付き丸棒とは

まず最初に段付き丸棒について解説します。

段付き丸棒とは、異なる直径の部分が連続している丸棒のことです。

段付き丸棒は、機械部品や構造物の一部として使用されることが多く、特に応力集中を避けるために設計されています。

主な用途

段付き丸棒は主に以下のような用途で使用されています。

①機械部品

付き丸棒は機械部品の製造において非常に有用です。特に異なる直径の部分を持つことで、部品同士の組み合わせや接続が容易になります。これにより、複雑な形状の部品を一体成形することが可能となり、製造コストの削減や組み立て作業の効率化が図れます。また、強度や剛性を必要とする部品にも適しており、耐久性が高いこともメリットです。

②構造物

段付き丸棒は、構造物の建設等に利用されます。段差のある形状は特定の力を分散させることができ、建物や橋などの構造物において安定性を向上させます。また、段付きの形状により他の部材との接合が容易になり、施工の効率が向上します。これにより耐震性や耐荷重性を高めることができるため、安心して使用できる構造物を建てることができます。

③自動車部品

自動車産業においても段付き丸棒は広く使用されています。エンジン部品やシャシー部品など、多くの自動車部品は高い強度と軽量化が求められていますので、この段付き丸棒が重宝されます。段付きの設計を施すことで、部品の軽量化を図りながらも必要な強度を保持することができ、結果として自動車全体の性能向上に貢献します。また、製造プロセスにおいても段付き丸棒を利用することで、部品の適合性や組み立て精度が増し、全体の品質を高めることができます。

段付き丸棒を使用するとどんなメリットがあるの？

そんないろいろな用途で使われている段付き丸棒ですが、それぞれの段の高さや直径が異なることを利用して、以下のようなメリットがあります。

①取り扱いやすさ

段差を設けることによって、他の部品との接続が簡単になる組み立てやすさがこの段付き丸棒の一番のメリットです。特に段付き部分がガイドになって正確に位置決めをすることができるため、組み立て作業がスムーズに進んだりするメリットがあります。

また、普通の丸棒と比べて段差になっているので滑り止め効果もあり、工具や手が滑りにくくなるというところも作業者の安全性を確保するというポイントにおいて、滑り止め効果の利点が発揮されます。

②耐久性の向上

段差部分があることで、応力(外部からかかる力)が均等に分散されやすくなります。これにより、特定の部分に過度な力が集中するのを防ぎ、部品全体の耐久性が向上します。ちなみにこの応力を分散させることを材力界隈ではよく「応力分散」といいます。

また、段付き丸棒はそれぞれ異なる直径を持つ部分があるため、用途に応じて強度を最適化することができます。

どうゆうことかというと、例えば大きな力がかかるようなところには太い部分で設計し、そんなに大きな負荷がかからないところor軽量化を図りたい場合は細い部分として設計することで、全体の重量を減らしつつも必要な強度を確保することができます。

さらに、段差部分が応力集中を分散する役割を果たすため全体として耐久性が向上し、長期間にわたって安定した性能を維持することができます。

ここの設計の考え方については安全率を考慮することで、信頼性の高い製品を実現することができるだけでなく、予期せぬ負荷(例えば衝撃荷重など)や使用条件の変動に対しても十分な強度を持たせることができます。(安全率については今回は取り扱わず、別記事で詳しく書こうと思います。)

段付き丸棒は一見あんまり身の回りになさそうな部品ですが、意識して見渡してみると実は多くの工業製品や日常用品に広く使われている部品なのです。

私がぱっと思いついたのは、射出成型機のシリンダー部分ですね！先端の部分は細いサイズになっていて、射出用加熱シリンダーのほうが大きいサイズになっているので、パッと見ドでかい段付き丸棒のような形になっています。このような形状にしたのも、もしかしたら大きな力(射出圧力)がかかるところには太い部分で設計し、そんなに大きな負荷がかからないところor軽量化を図りたいところ(溶けた樹脂の流路部分)は細い設計にするという意図があってこのような形なのかもしれませんね。

次の項目では、その段付き丸棒の計算問題について一緒に考えていきたいと思います。

計算問題

例題

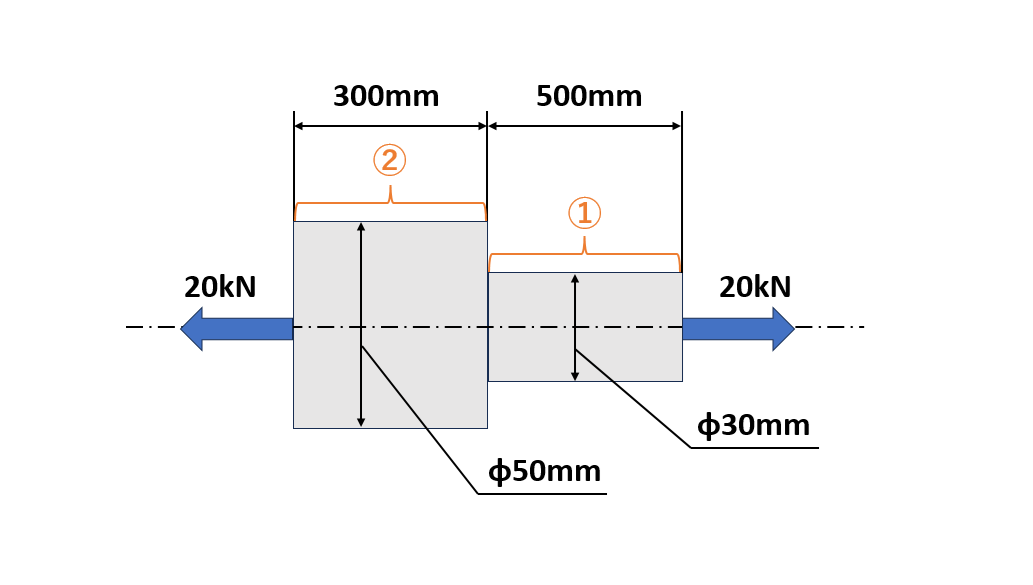
直径30mmと直径50mmの段付き丸棒に20kNの引張荷重が作用している。このときこの材料の縦弾性係数を206GPaとして図AとBの部分に発生する応力と全体の伸びを求めなさい。

例題の解答

まず①と②それぞれの応力を求めます。

①の応力について

$$σ1=\frac{P}{A}=\frac{\frac{P}{1}}{\frac{πD^2}{4}}=\frac{4P}{πD^2}$$

$$=\frac{4×20×10^3}{π×30^2}$$

$$=28.30MPa　・・・(1)$$

②の応力について

$$σ2=\frac{P}{A}=\frac{\frac{P}{1}}{\frac{πD^2}{4}}=\frac{4P}{πD^2}$$

$$=\frac{4×20×10^3}{π×50^2}$$

$$=10.19MPa　・・・(2)$$

次に①と②それぞれの伸び(λ)をもとめます。縦弾性係数Eは

$$縦弾性係数E=\frac{σ}{ε}=\frac{\frac{P}{A}}{\frac{λ}{l}}=\frac{Pl}{Aλ}$$

と式変形でき、これをさらに式変形するとλが求められそうですね。なのでこの式を使ってλ＝という形に直します。

$$縦弾性係数E=\frac{Pl}{Aλ}$$

$$\frac{A}{Pl}×E=\frac{Pl}{Aλ}×\frac{A}{Pl}$$

$$\frac{AE}{Pl}＝\frac{1}{λ}$$

$$λ＝\frac{Pl}{AE}　・・・(3)$$

断面積Aの形状は円なので、ここに

$$A＝\frac{πd^2}{4}$$

を代入すると

$$λ＝\frac{Pl}{AE}＝\frac{\frac{Pl}{1}}{\frac{πd^2E}{4}}=\frac{4Pl}{πd^2E}　・・・(4)$$

が得られます。これをつかってそれぞれの伸びを計算すると

①の伸び

$$λ＝\frac{4Pl}{πd^2E}＝\frac{4×20×10^3×500}{π×30^2×206×10^3}$$

$$=0.068675=0.07mm　・・・(5)$$

②の伸び

$$λ＝\frac{4Pl}{πd^2E}＝\frac{4×20×10^3×300}{π×50^2×206×10^3}$$

$$=0.014834=0.01mm　・・・(6)$$

となる。ここで注意してほしいのは、縦弾性係数Eは206「G」Paなので、MPaに置き換えて計算すると数値は「206×10^3」となります。

最後に全体の伸びを計算します。①の部分の伸びと、②の部分の伸びの和が全体の伸びとなる、ということだったので

λ＝λ₁+λ₂＝＝0.07+0.01=0.08mm　・・・(7)

解

①の応力：28.30MPa

②の応力：10.19MPa

全体の伸び：0.08mm

別解

①と②の部分についての応力が計算できているので、この計算結果を利用してそれぞれの伸び(λ)を次のような手順で表すことができます。

まず、縦弾性係数Eの式は

$$縦弾性係数E=\frac{Pl}{Aλ}$$

式変形すると

$$λ＝\frac{Pl}{AE}$$

でしたね。この式の中の右辺には

$$\frac{P}{A}$$

という分数が含まれています。これは応力の公式の

$$σ＝\frac{P}{A}$$

に相当するので、ここをσに置き換えれば、さっき得た計算結果を使って伸びの計算ができるようになります。

したがって

$$①の伸び：λ＝\frac{Pl}{AE}＝\frac{l}{E}×σ$$

$$＝\frac{28.30×500}{206×10^3}=0.068689=0.07mm$$

$$②の伸び：λ＝\frac{Pl}{AE}＝\frac{l}{E}×σ$$

$$＝\frac{10.19×300}{206×10^3}=0.014840=0.01mm$$

となります。

この方法で計算した場合、応力の数値は実数ではなく近似値になるため、上の解法で求めた値と少し異なる場合がありますが、極端に数値が変わるわけではありませんので安心してください！なので厳密な数値を求めたい場合は上の解法で計算してください。

まとめ

段付き丸棒は、さまざまな用途に応じた優れた素材です。その特性を把握し適切に活用することで、製品の品質向上やコスト削減を実現させることができます。

今後も新しい技術や応用方法が登場すると思うので、今回の内容と段付き丸棒の可能性を探求し続けることを頭の片隅に入れておくと、画期的なアイデアが出てくるかもしれません。

ぜひ、あなたのプロジェクトにおいても段付き丸棒を取り入れて、より良い成果を目指してください。