熱ひずみと熱応力は非常に重要な概念です。これらは材料が温度変化にさらされたときに生じる変形や内部応力のことを指し、特に工業製品や建築物の設計において無視できない要素となります。
たとえばエンジン部品や航空機の構造材料は、運転中に大きな温度変化にさらされるため、熱ひずみと熱応力の影響を解析することが不可欠です。これを怠ると破損や変形といった深刻な問題を引き起こす可能性があります。
さらに近年では材料の高性能化が進んでおり、複合材料や新しい合金などの開発が盛んに行われています。
これらの材料は、熱に対する反応が従来の材料とは異なるため、熱ひずみや熱応力の理解がますます重要になっています。
本記事では、熱ひずみと熱応力の基本的な概念を詳しく解説し、それらがどのように材料や構造物の性能に影響を与えるのかを探っていきます。
これにより皆さんが実際の設計や解析に役立てられる知識を提供できればと考えています。
熱ひずみとは
熱ひずみとは、物体が温度の変化によって形状や寸法の変化が発生することをいいます。
金属の棒を加熱すると、棒が少しだけ長くなります。逆に冷却すると棒は縮みます。このような変化は構造物や機械の設計において考慮する必要があり、熱ひずみが大きくなると物体の強度に影響を与えることもあるため、特に重要な現象です。
棒状の材料では、体積変化のほとんどが長さの変化になります。例えば長さl(エル)の棒材があったとして、この棒材が温度t1からt2への温度変化があったとすると、線膨張係数α(アルファ)を比例定数としてΔtに比例した変化量λが発生します。
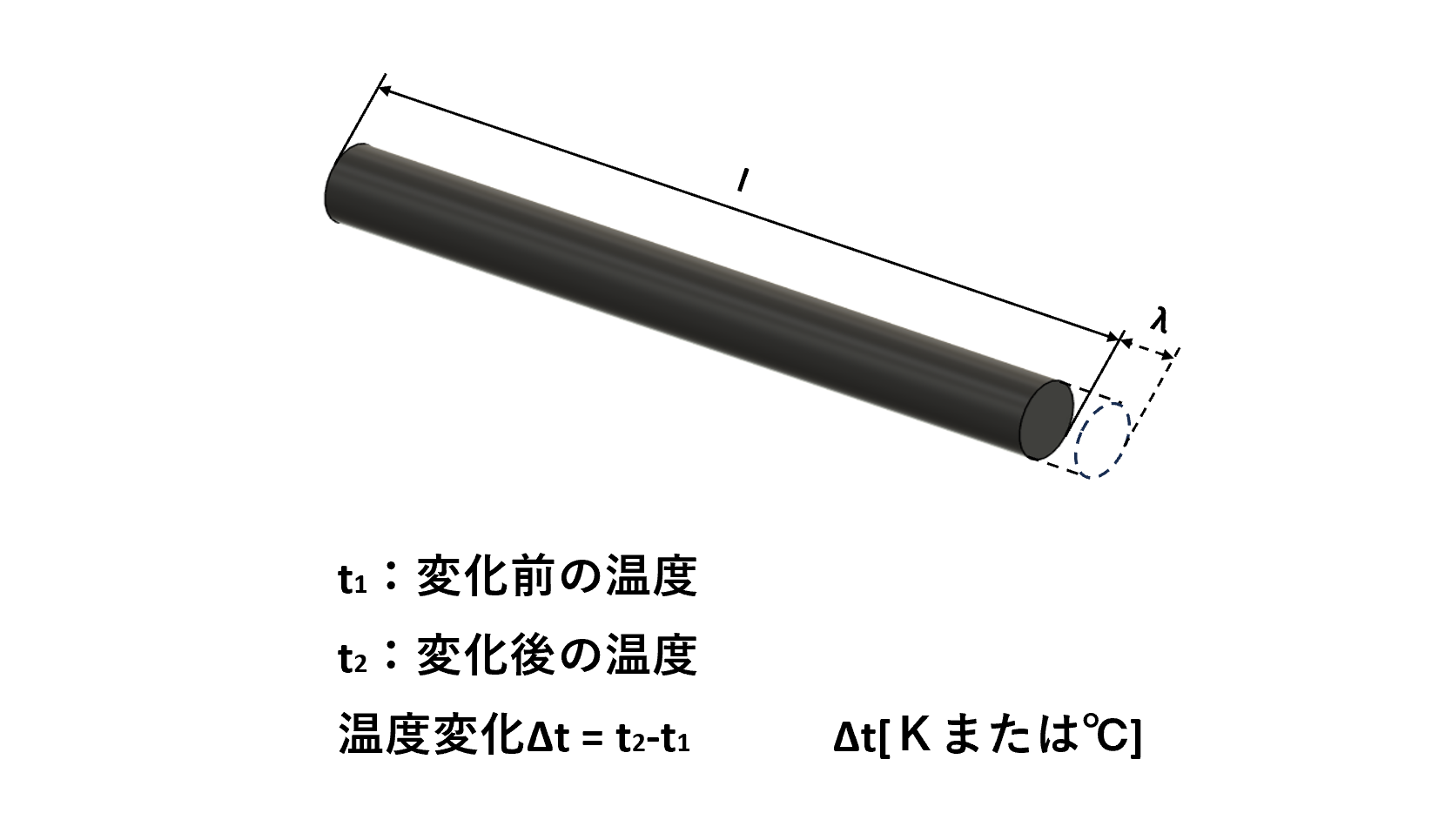
t1からt2への温度変化は、
$$Δt=t_{2}-t_{1}$$
となり、変化量λは次式で表すことができます。
$$λ=αlΔt ・・・(1)$$
そして、変化量λを長さlで割った値が熱ひずみです。記号はε(イプシロン)で表します。
$$ε=\frac{λ}{l}$$
ここで分子のλに式(1)を代入すると以下の関係式が成り立ちます。
$$熱ひずみε=\frac{λ}{l}=\frac{αlΔt}{l}=αΔt ・・・(2)$$
線膨張係数
線膨張係数とは、材料が温度変化に応じてどの程度膨張(収縮)するかを示す指標で、材料の長さが1度の温度変化によってどれだけ変化するかを表します。
JIS規格では単位はケルビンK(1/K)と規定されていますが、℃(1/℃)と表すこともあります。
ちなみに線膨張係数の単位をケルビン(1/K)から摂氏(1/℃)に変換しても数値は同じになります。
なぜ数値が同じかというと、それは摂氏温度(℃)と絶対温度(K)の間に一定の差(273.15K)があるものの、温度差を表す際には同じ間隔で増加するためです。したがって数値を変更する必要はありません。
建築分野では「1/℃」が一般的に使用されることが多いですが、CAE(コンピュータ支援工学)などの解析分野では「1/K」がよく使われます。これは解析ソフトウェアや物理モデルが絶対温度(K)を基準にしているため、より一貫性のある計算が可能になるからです。よって各分野の慣習に応じて単位が選ばれることが多いです。
また、材料は温度が上昇すれば膨張し、温度が低下すると収縮する体積変化を起こします。材料の軸方向に変化する度合いを単位体積当たりのひずみで表したものを線膨張係数α(アルファ)と呼びます。
線膨張係数の用途と係数一覧
線膨張係数は主に機械や建築材料の設計において、温度変化による寸法変化を予測するために活用されます。
以下に、一般的な材料の線膨張係数の一覧を示します。
| 材料 | 線膨張係数(10-5/℃) |
| 鋼 | 1.2 |
| ステンレス | 1.7 |
| アルミニウム | 2.4 |
| ポリスチレン(PS) | 6~8 |
| ポリプロピレン(PP) | 5.8~10.2 |
| 鋳鉄(FC200) | 1.15~1.20 |
プラスチックの熱膨張率は金属に比べて約一桁大きく、セラミックスに対しては二桁以上も異なります。これは熱によって、長さや体積が大きく変化する材料であることを示しています。
プラスチックはもともと高温環境にはあまり適していない材料ですが、一般的なプラスチックでも約100℃前後の耐熱性を持つものがあります。そのため、部品として使用する際にはこの熱膨張を考慮して設計を行うことが重要です。
また、温度変化が頻繁にある環境では、適切な遊間(すきま)を確保することで応力の発生を防ぎ、材料の破損や変形を避けることができます。
異なる材料を組み合わせる場合、各材料の線膨張係数を考慮することで、接合部の信頼性を高めることができます。
熱応力
熱応力とは、温度の変化によって材料内部に生じる応力のことです。
具体的には材料が熱膨張や収縮をする際に、周囲の制約や接合部分などによって材料が拘束されていて自由に動けない場合に発生します。
物体にはそれぞれ固有の線膨張係数があり、温度が上がると膨張し、下がると収縮します。
しかし、温度変化による膨張や収縮する物体が拘束されていると、自由に変形できる場合に生じる変形量がひずみとなり、物体内部に残留して応力が発生します。
この応力は外部からの力によって生じるものではなく、温度の変化によって引き起こされるため、「熱応力」と呼ばれます。
熱応力の導出
断面積Aの材料を両端で固定し温度変化Δtを加えると自由に膨張や収縮できないため、拘束された部分で長さの変化が生じます。
この変化によって、材料内部に軸方向の荷重Pが発生します。ここで、材料に垂直応力σ0、弾性ひずみε0が発生すると考えます。
つまり、温度変化によって引き起こされる長さの変化が、固定された状態では自由に動けないために応力として蓄積されているということです。
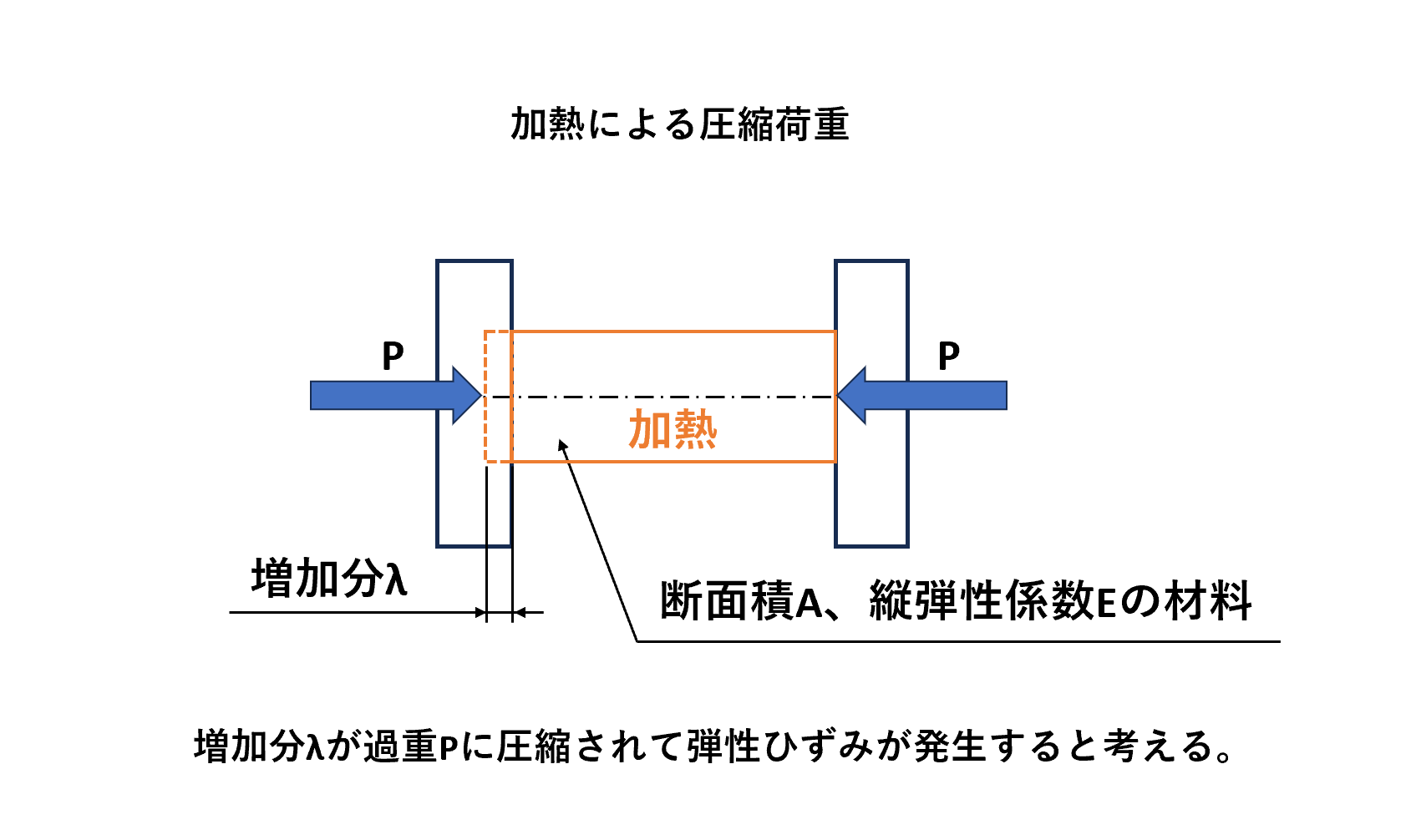
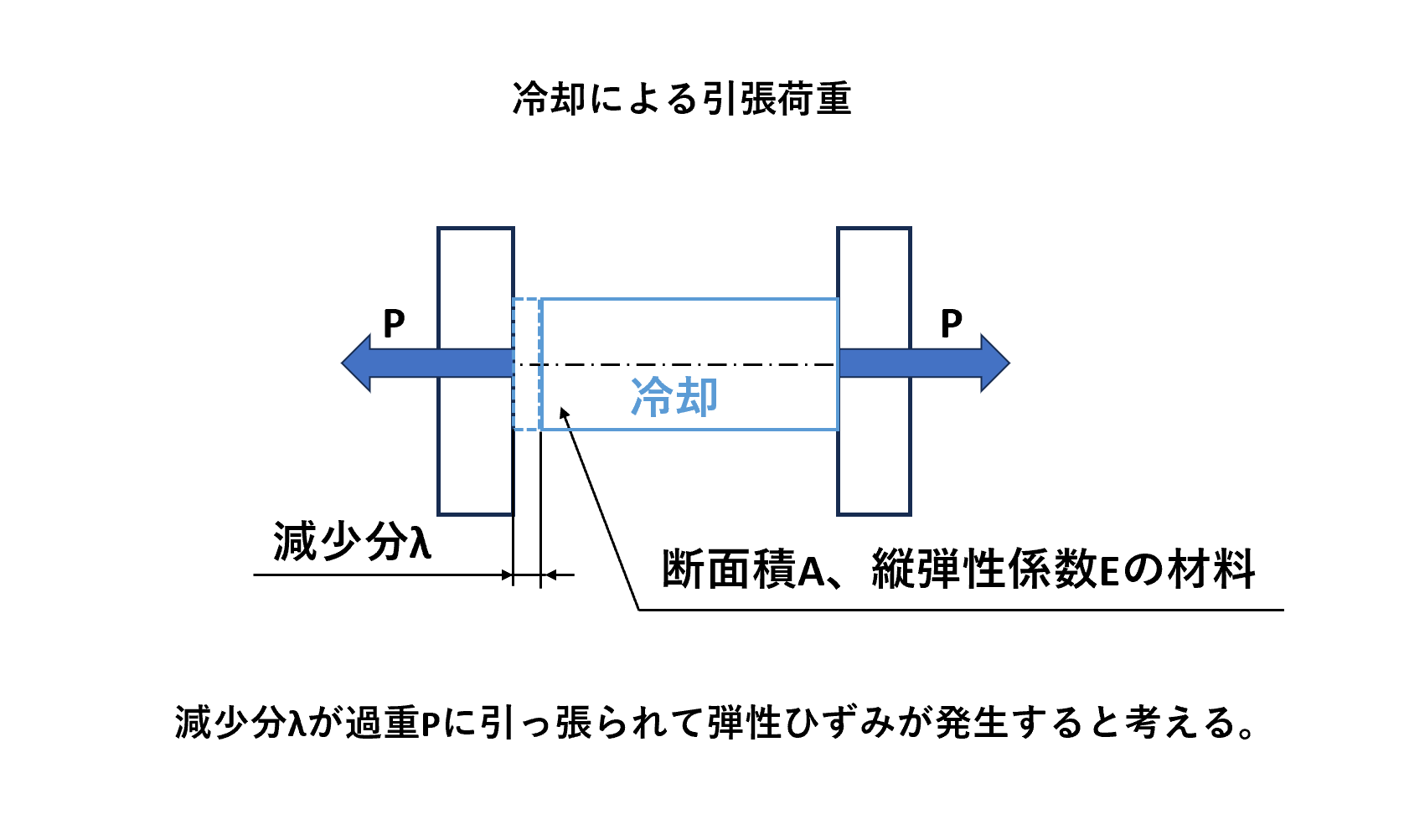
上記の内容をおさえて熱応力σを導きます。
垂直応力は、
$$σ_{0}=\frac{P}{A} ・・・(3)$$
縦弾性係数は、
$$E=\frac{σ}{ε} ・・・(4)$$
であり、式(4)を式変形すると、
$$E=\frac{σ}{ε}$$
$$E×\frac{1}{σ}=\frac{\cancel{σ}}{ε}×\frac{1}{\cancel{σ}}$$
$$\frac{E}{σ}=\frac{1}{ε}$$
$$ε=\frac{σ}{E} ・・・(5)$$
となります。ここで、式(5)のσに式(3)を代入すると、
$$弾性ひずみε_{0}=\frac{σ_{0}}{E}=\frac{\frac{P}{A}}{E}=\frac{P}{AE} ・・・(7)$$
が得られます。
両端が固定されている部材の変形量は変わらないので、部材に発生する熱ひずみεと弾性ひずみε0の和はゼロとして、部材に発生する熱応力σは次のように考えます。
式(2)の熱ひずみと式(5)の弾性ひずみの和が0となる式をつくるので、
$$ε+ε_{0}=αΔt+\frac{P}{AE}=0 ・・・(6)$$
式(6)を荷重Pについての式に変形すると、
$$αΔt+\frac{P}{AE}=0$$
$$αΔt×AE+\frac{P}{\cancel{A}\cancel{E}}×\cancel{A}\cancel{E}=0$$
$$αΔtAE+P=0$$
$$P=-αΔtAE ・・・(7)$$
が得られます。そして応力の式、
$$σ=\frac{P}{A}$$
の分子Pに式(7)を代入すると、
$$σ=\frac{P}{A}=\frac{-αΔtAE}{A}=-EαΔt$$
が得られ、これが熱応力となります。
加熱においてはΔtが正となりますので熱応力σは負となり、部材に圧縮応力が発生していることを示します。逆に冷却ではΔtが負で熱応力σは正となるので、引張応力が発生していることを示します。
次の項目からは熱による伸縮と、熱応力を受ける材料の計算問題について扱っていきます。
計算問題
例題1(軸に沿った応力)
等間隔で固定された2つの剛体壁がある。伸縮可能な段付き軸が一方の壁から通され、もう一方の端は固定されている。温度が320℃のとき、軸の首下長さは1mで、壁との間に1mmの隙間があるとする。軸の温度が250℃に下がった場合、軸はどのように変化するかを答えなさい。材料の縦弾性係数は206GPa、線膨張係数は1.5×10⁻⁵/Kとする。
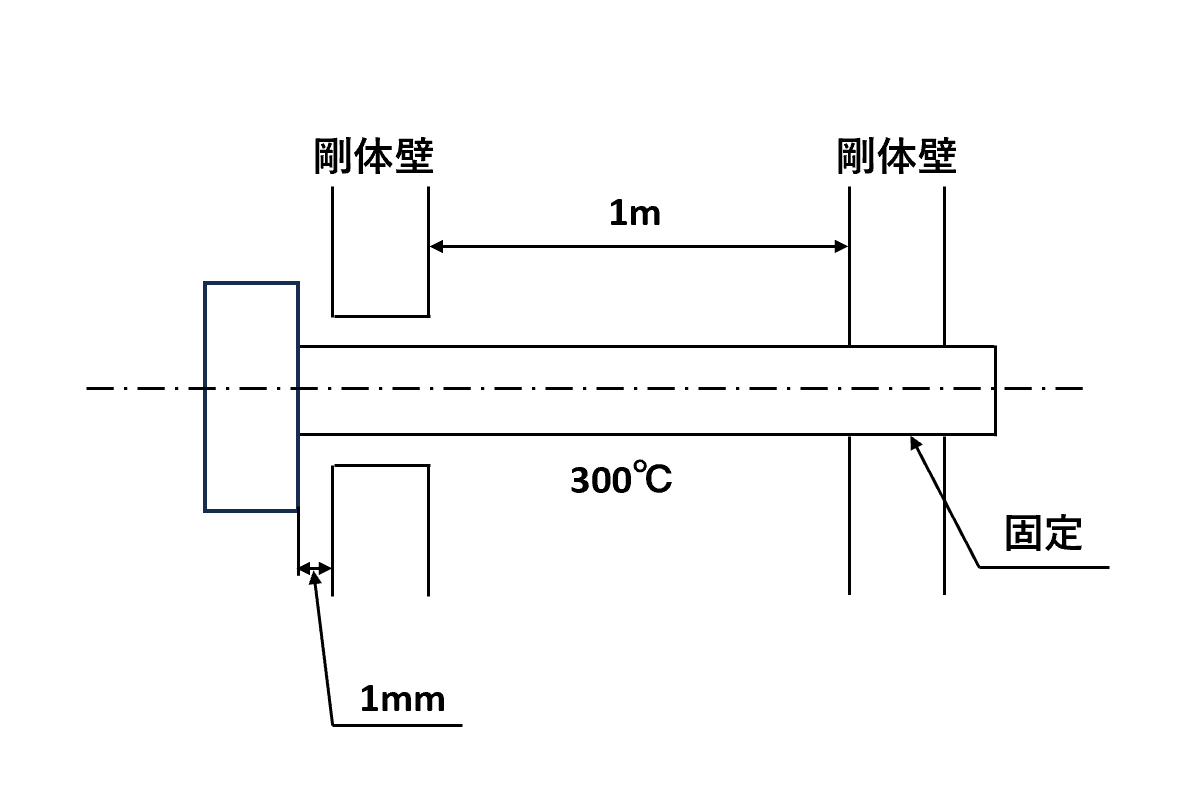
今回の内容のキーポイント
今回は以下の手順で軸がどのように変化するかを求めていきます。
- 収縮量が1mmになるときの温度t2を求める。
- もしt2が250℃に達しない場合、さらに収縮が進み熱応力が発生することになる。
- t2から250℃までの間に生じる垂直応力を計算する。
温度が下がることによって段付き軸が収縮する量を計算します。線膨張係数を用いて、温度変化に伴う長さの変化を求めます。この時λの符号は伸びを正、収縮を負と置きます。具体的には、式(1)を使ってt2を求めていきます。
$$λ = αlΔt=αl(t_{2}-t_{1})$$
この式からt2が決まるので、この数値を用いて計算を進めていきます。
次に収縮量と比較して隙間(1mm)がなくなるかどうかを確認します。t2が250℃に達しない場合、段付き軸は収縮し続けその結果、軸と壁の間の隙間がなくなります。このとき、軸が固定されているためさらに収縮することができず、ここで熱応力が発生します。
最後に、温度t2から250℃までの間に発生する熱応力を計算します。熱応力は、以下の式で求めることができます。
$$σ=-EαΔt$$
例題1の解答
収縮量1mmの時の温度t2を式(1)を使って求めます。
$$変形量λ = αlΔt=αl(t_{2}-t_{1})$$
$$=αlt_{2}-αlt_{1}$$
$$λ×\frac{1}{αl}=\cancel{α}\cancel{l}t_{2}×\frac{1}{\cancel{α}\cancel{l}}-\cancel{α}\cancel{l}t_{1}×\frac{1}{\cancel{α}\cancel{l}}$$
$$\frac{λ}{αl}=t_{2}-t_{1}$$
$$t_{2}=t_{1}+\frac{λ}{αl}$$
$$=320+\frac{-1}{1.5×10^{-5}×1×10^3}=253.33℃$$
1mm収縮した時の温度が250℃まで達しないため、t2=253.33℃からt3=250℃までの温度変化における熱応力について考えます。
$$熱応力σ=-EαΔt=-Eα(t_{3}-t_{2})$$
$$=-206×10^3×1.5×10^{-5}×(250-253.33)$$
$$=10.2897・・・=10.29MPa$$
解:温度が320℃から250℃に変化した軸は拘束され収縮できず、10.29MPaの引張応力が発生する。
例題2(鉄道レールの伸縮に関する問題)
鉄道のレールは温度変化による伸縮に対応するため、レールの接合部に「遊間」と呼ばれる適度な隙間を設けています。長さ25mの定尺レールが40℃の時に隙間がゼロで接触していると仮定します。このレールが自由に伸縮できる状態で、温度が-10℃の時の遊間と60℃の時に発生する応力を求めなさい。材料の縦弾性係数は206GPa、線膨張係数は11.5×10-6/Kとします。
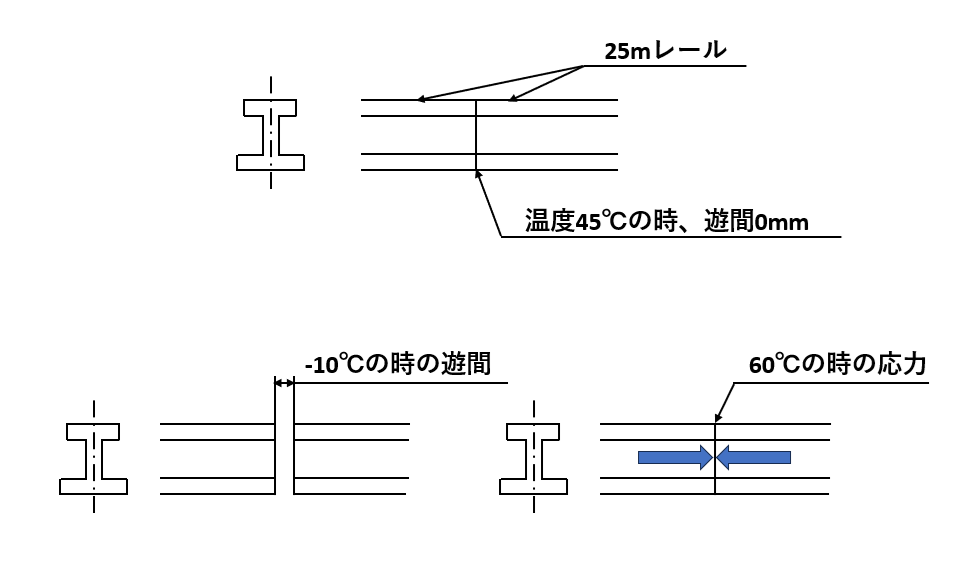
ポイント
- 温度低下によるレール1本の収縮量を、遊間の増加量とする。
- レールが冷却されると、温度が下がることでレールの長さが縮む現象が起こります。この収縮量は、レールの材質や温度変化の大きさに依存します。遊間(すきま)がゼロの状態から始まるため温度が-10℃に下がった時に、レールが縮む分だけ遊間が増加することになります。つまり、レールの収縮によって遊間がどれだけ広がるかを計算することで、温度低下に伴う影響を把握します。温度が-10℃の時、どのくらいの遊間があるのかについては下記の式を使って解いていきます。
$$変形量λ = αlΔt=αl(t_{2}-t_{1})$$
※長さlの単位に注意して式に代入。
- レールが冷却されると、温度が下がることでレールの長さが縮む現象が起こります。この収縮量は、レールの材質や温度変化の大きさに依存します。遊間(すきま)がゼロの状態から始まるため温度が-10℃に下がった時に、レールが縮む分だけ遊間が増加することになります。つまり、レールの収縮によって遊間がどれだけ広がるかを計算することで、温度低下に伴う影響を把握します。温度が-10℃の時、どのくらいの遊間があるのかについては下記の式を使って解いていきます。
- 温度上昇によるひずみが拘束されて、圧縮応力を生む。
- レールの温度が上昇するとレールは膨張しようとしますが、隙間がない状態ではその膨張が制約されます。この制約によってレール内にひずみが生じ、さらにそれが圧縮応力として蓄積されます。よって、温度が60℃に上昇した際、レールがこれ以上自由に伸びることができず、その結果として内部に圧縮応力が発生します。ここは以下の式を適用していきます。
$$σ=-EαΔt$$
- レールの温度が上昇するとレールは膨張しようとしますが、隙間がない状態ではその膨張が制約されます。この制約によってレール内にひずみが生じ、さらにそれが圧縮応力として蓄積されます。よって、温度が60℃に上昇した際、レールがこれ以上自由に伸びることができず、その結果として内部に圧縮応力が発生します。ここは以下の式を適用していきます。
例題2の解答
定尺レールが-10℃の時の遊間
$$変形量λ = αlΔt$$
$$=αl(t_{2}-t_{1})$$
$$=11.5×10^{-6}×25×10^3(-10-40)$$
$$=-14.38mm$$
※計算結果がマイナスなので、-14.38mmレールの長さが収縮したということになる。
定尺レールが60℃の時の応力
$$σ=-EαΔt$$
$$σ=-Eα(t_{2}-t_{1})$$
$$=-206×10^3×11.5×10^{-6}(60-40)$$
$$=-47.38MPa$$
※計算結果がマイナスなので、圧縮応力47.38MPa発生したということになる。
解:定尺レールが-10℃の時の遊間 14.38mm、定尺レールが60℃の時に発生する圧縮応力 47.38MPa
まとめ
今回は熱による材料の変形や熱応力に関する問題を扱いました。
材料が変形する原因は外力だけではなく、温度の変化による体積の変化も影響しています。
機械設計では温度変化の影響で材料が変形することを想定した適切な構造計算が必要となりますので、今回の問題はしっかりと習得しておいてください。
この記事はこれで終了です。最後までお読みいただき、ありがとうございました。
