材料力学において『応力集中』は、構造物の安全性や耐久性に大きな影響を与える重要な概念です。
応力集中とは特定の形状や欠陥によって発生する局所的な応力の増加を指し、これが原因で材料が破損することがあります。
本記事では応力集中の基本的な概要からその実例、計算方法について解説します。
応力集中を理解することで、より安全で信頼性の高い構造物の設計が可能になります。
応力集中とは
応力集中とは部材に引張荷重などの外部からの荷重が発生したとき、切り欠きや穴、その周辺で応力が局所的に集中する現象のことを指します。
通常、材料にかかる力は均等に分散されますが繰り返し荷重などの動荷重が発生したり、形状の変化や欠陥がある場合、その部分に応力が集中し周囲の部分よりも高い応力がかかることになります。
そのため応力集中の度合いは、断面形状の変化が著しいほど大きくなります。
材料に引張応力をかけた場合の応力集中の分布は、図で表すと以下のような結果になります。
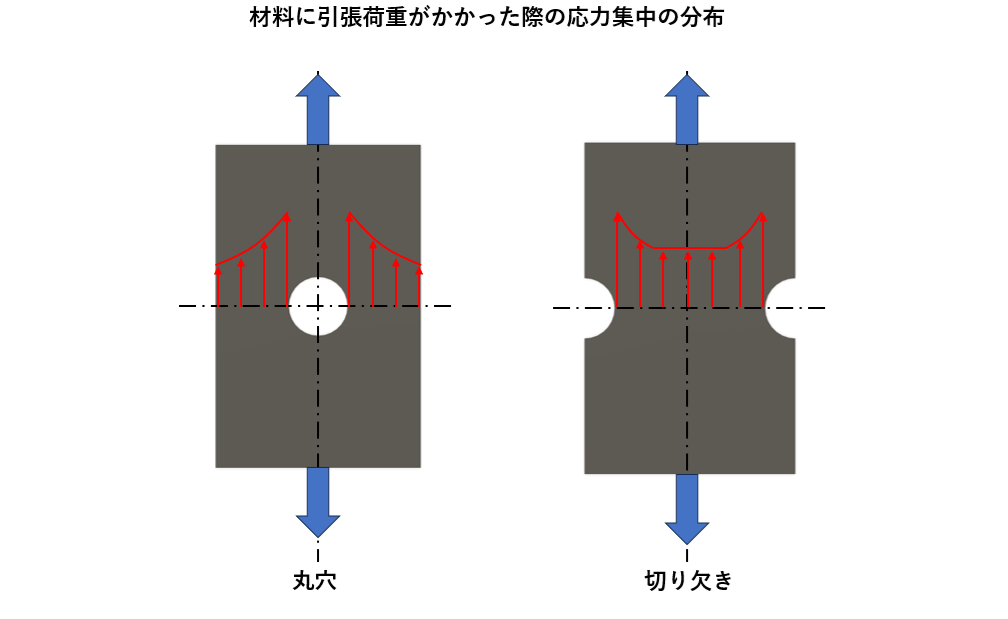
左側の図で板に穴が開いている形状の場合、穴の近傍では応力は大きくなり、穴から遠ざかるに従い応力が小さくなります。
応力集中を避けるための方法
急激な形状変化があるところに応力集中が起ることから、応力集中を避けるために下記のような対策をとる必要があります。
1. 円弧やフィレットを使って形状の最適化
角がある部分を丸めること(フィレットの追加)で、応力が集中しにくくなります。端面が直角な部材よりも、円弧やフィレットを使った部材が効果的です。
2. C面取りの追加
C面取りを追加することで、端面が直角な部材よりも応力集中を軽減できます。
3. 逃げ溝(アンダーカット)の追加
フランジ部品などの根元にはR形状が施されており、この円弧を描くようななだらかなR局面をつけることで応力集中を緩和します。
4. 断面積を増やす
応力が集中しやすい部分の断面積を増やすことで、応力を分散させることができます。例えば、部材の直径を増やすことがあげられます。
5. 適切な接合方法
溶接やボルト締結などの接合部に関しても応力集中が起こりやすいので、接合方法や接合部の形状を工夫することが重要です。例えば、ボルトの頭部を大きくして単位面積あたりにかかる力を分散させておくなどの工夫があげられます。
高靭性材料の選定も間接的な応力集中対策となる。
応力集中を避けるための直接的な対策というわけではないですが、応力集中が懸念される部分に靭性の高い材料を選ぶことで、破壊に対する耐性を向上させることができます。機械部品に広く使用されている鋼材、航空機や車両の構造材などに利用されているアルミニウム合金、柔軟性があり軽量かつ靭性が高い繊維強化プラスチックなどの材料を選定することで局所的な応力集中が発生したとしても材料が持つ強い靭性によって部材の破壊を避けることができます。
形状係数について
次に形状係数について解説します。ここでは部材の中心に丸穴がある形状を例に記載します。
形状係数(応力集中係数)とは、穴の近傍で局所的に増大している最大応力(σmax)を、集中応力を考えずに最小断面を基準に一様に分布すると仮定した平均応力(σn)で割った値のことです。
形状係数の記号はα(アルファ)で、式で表すと以下のような関係になります。
$$形状係数α=\frac{最大応力σ_{max}}{平均応力σ_n}$$
平均応力σnは応力集中を無視した最小断面積で割った値であり、以下の式で求めることができます。
$$平均応力σ_n=\frac{P}{(D-d)t}$$
P:荷重
D:材料の幅
d:穴の直径
t:板厚
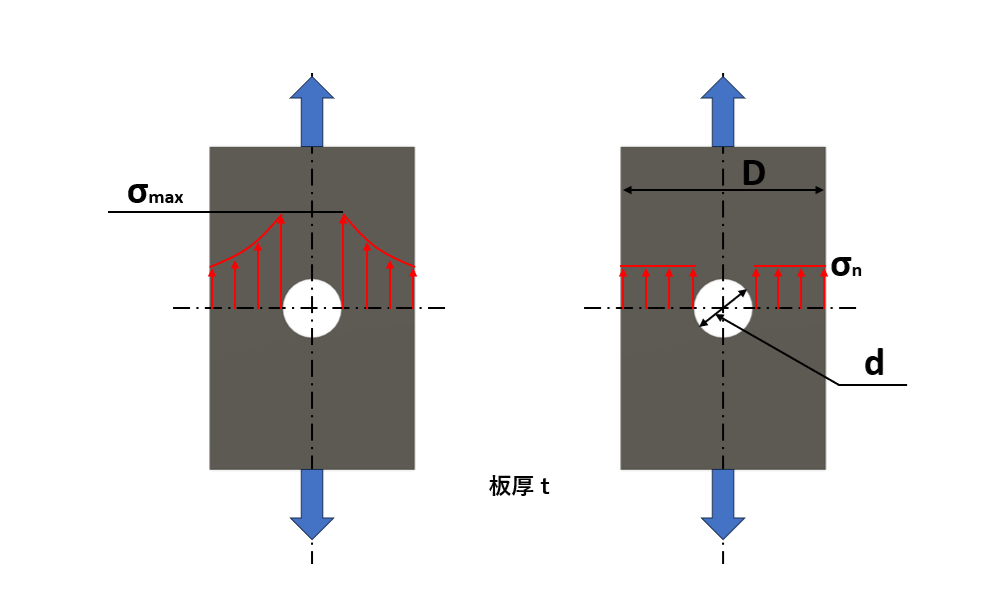
形状係数の使用例
形状係数は材料の形状と荷重条件によって決まる数値なので、実験数値や計算値をもとにして、次のような表より求めます。
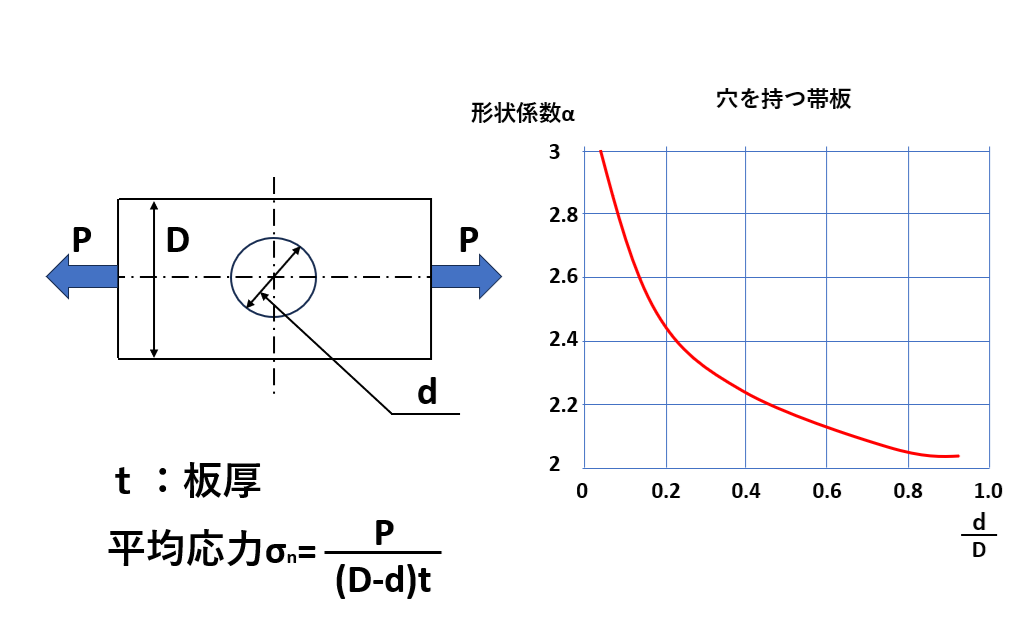
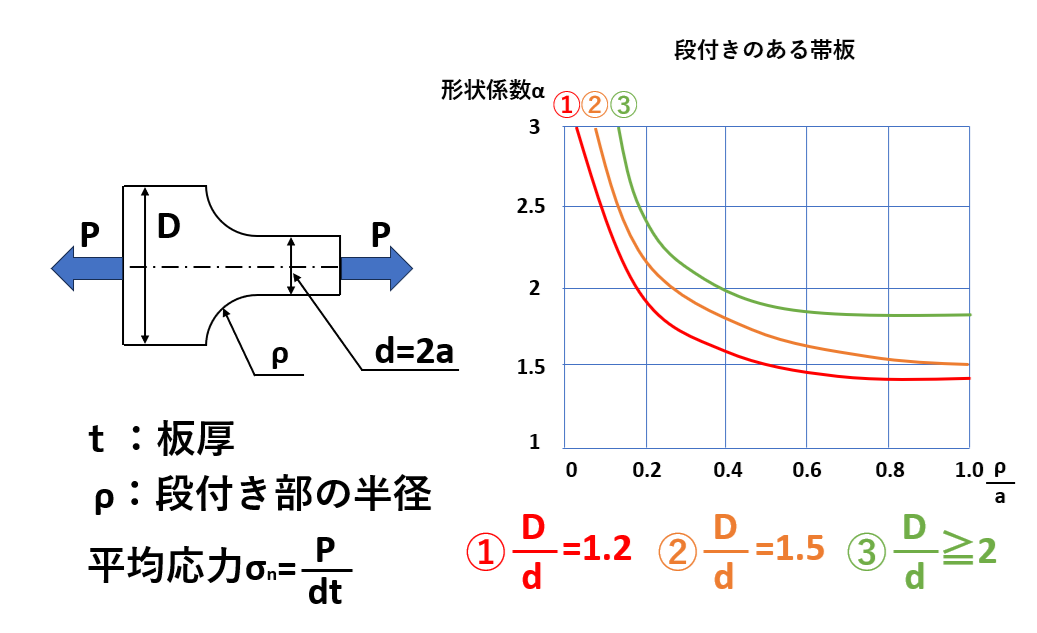
形状係数の求め方は、上図を参考にして次のような手順で決めていきます。
穴を持つ帯板の形状係数の求め方
例えば、幅70mm、穴の直径20mmの場合、次のように求めます。
$$\frac{d}{D}=\frac{20}{70}=0.29≒0.3$$
次に0.3と横軸の数値が合致しているところを見つけます。
最後に縦軸を見ます。実験値の曲線が重なる箇所が形状係数αとなります。
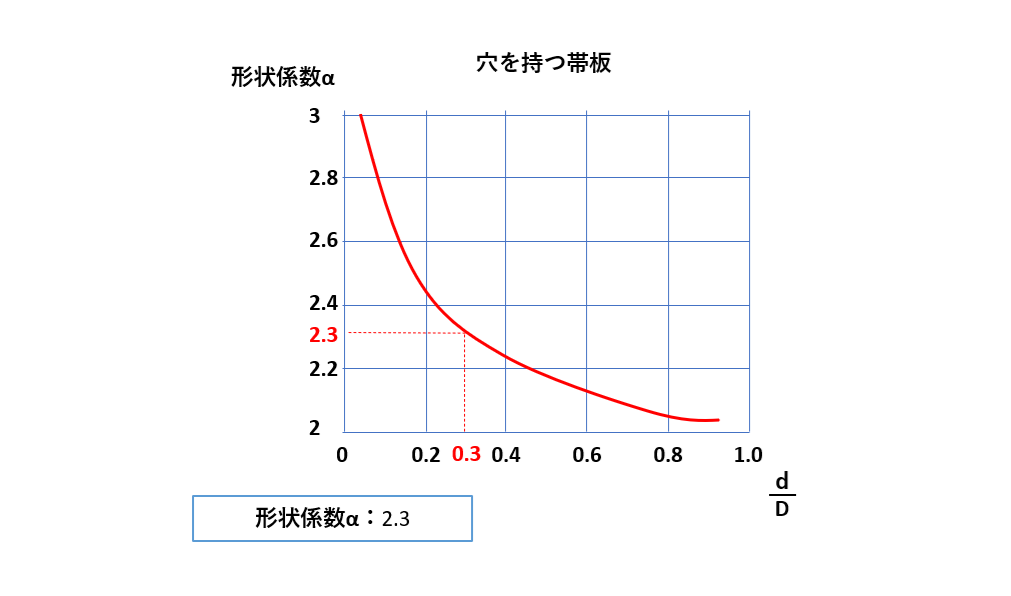
形状係数を使うことでどこに応力が集中しているのか、その度合いを知ることができます。
材料力学における形状係数は、構造物の強度や剛性を評価するための重要な要素で、荷重が断面の形状や寸法にどのように影響するかを具体的に示す数値となります。
計算問題
例題1
幅100mm、厚さ5mm、中央に直径20mmの穴を持つ板材(帯板)に、5kNの引張荷重が作用している。このときに発生している最大応力を求めなさい。
ポイント
①最初に平均応力σnを求めます。式は、
$$平均応力σ_n=\frac{P}{(D-d)t}$$
を使い、ここからσnを導出します。
②幅100mm、直径20mmの数値を使って「穴を持つ帯板」の表から形状係数αを決定し、最大応力σmaxを求めます。σmaxをもとめるために、
$$形状係数α=\frac{最大応力σ_{max}}{平均応力σ_n}$$
を使います。
例題1の解答
①平均応力σnを求めます。
$$平均応力σ_n=\frac{P}{(D-d)t}$$
$$平均応力σ_n=\frac{5×10^3}{(100-20)5}$$
$$=12.5MPa$$
②穴を持つ帯板の形状係数の表から形状係数αを求める。
幅100mm、直径20mmなので、
$$\frac{d}{D}=\frac{20}{100}=0.2$$
となり、形状係数αは2.45とする。
③最大応力を求める。
先ほど選定した形状係数α(2.45)を使って最大応力を求める。
$$形状係数α=\frac{最大応力σ_{max}}{平均応力σ_n}$$
$$σ_{max}=ασ_n=2.45×12.5$$
$$=30.6MPa$$
解:最大応力30.6MPa
例題2
幅D=120mm、幅d=80mm、厚さ4mmの段付きのある帯板鋼に10kNの引張荷重が作用している。安全率S=3としたとき、基準応力を200MPaとして段付き丸み部分の半径ρを求めなさい。
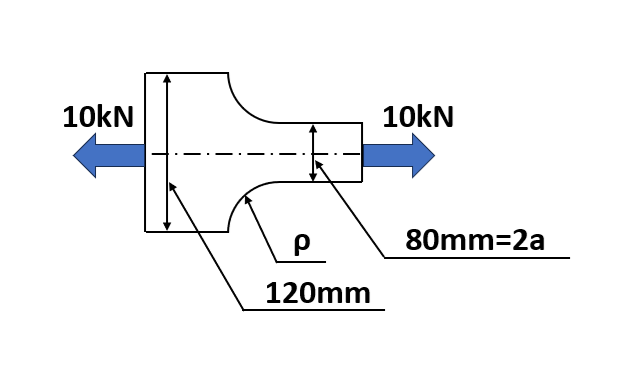
ポイント
許容応力を求める公式
$$σ_a=\frac{σ_a}{S}$$
のσaを最大応力σmaxとみなし、この材料の形状係数αを決定します。
そして形状係数αから
$$\frac{ρ}{a}$$
を求めて、段付き部の半径ρを求めます。
例題2の解答
σaを最大応力σmaxとおく。
$$σ_a=σ_{max}=\frac{σ_s}{S} ・・・(1)$$
段付きのある帯板の平均応力σnを求めるための式は、
$$σ_n=\frac{P}{dt} ・・・(2)$$
形状係数αを求める式、
$$α=\frac{σ_{max}}{σ_n}$$
に式(1)と式(2)それぞれを代入する。
$$α=\frac{σ_{max}}{σ_n}$$
$$=\frac{\frac{σ_s}{S}}{\frac{P}{dt}}$$
$$=\frac{σ_sdt}{SP}$$
$$=\frac{200×80×4}{3×10×10^3}$$
$$=2.13$$
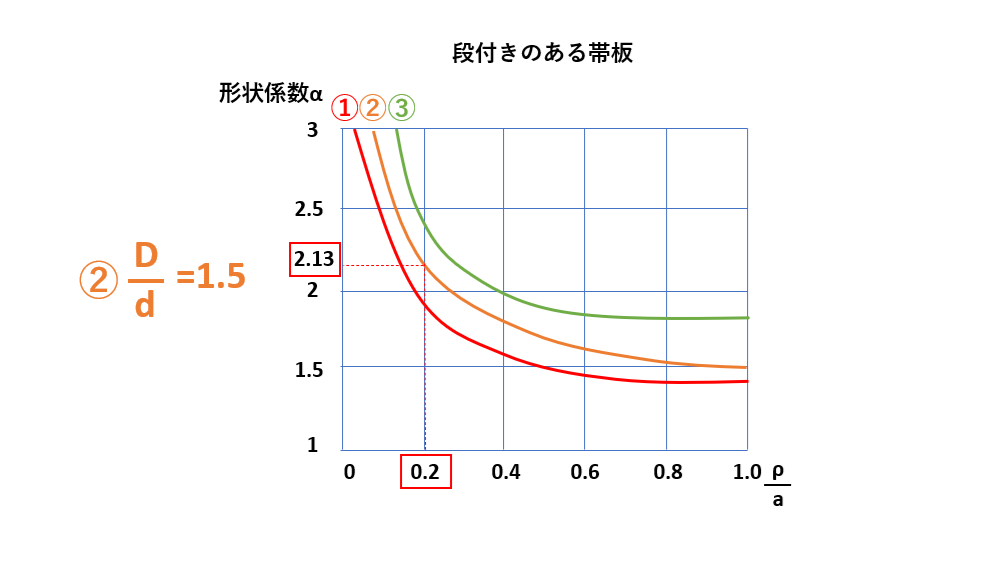
段付きのある帯板の表より、
$$\frac{D}{d}=\frac{120}{80}=1.5$$
となり、α=2.13からグラフの横軸を読み、
$$\frac{ρ}{a}=0.2$$
とする。d=2aより、80=2a、
$$a=\frac{80}{2}=40$$
が得られる。ここで得られた数値を用いて、
$$\frac{ρ}{a}=0.2$$
の式に代入すると、
$$\frac{ρ}{a}=0.2$$
$$ρ=0.2a=0.2×40=8mm$$
となる。
解:段付き丸み部分の半径ρ 8mm
まとめ
以上のことから形状係数と応力集中は構造物の設計において相互に関連しており、形状係数も一緒に覚えておくことで応力集中の影響を予測し、早期に対策を講じることができます。
