材料力学は構造物の設計や解析において不可欠な学問です。本記事では基本的な概念である「応力」をわかりやすく解説し、実際の計算に役立つ知識を提供します。
あなたのこれからの学びの旅をサポートし、理解を深める手助けをしていければなと思っています。
これから材料力学を学ぼうとしている皆さんが、自信を持って計算や設計に取り組むための第一歩を提供していきたいと思っていますので、一緒に知識を深めていきましょう。
応力とは?
応力(おうりょく)は、物体の内部に作用する力のことです。単位面積あたりにかかる内力を指します。物体に外力が加わると、その内部にはそれに対抗する力が生じます。力(P)を面積(mm2)で割ったものが応力です。
応力は英語で「Stress」と呼ばれ、工学や物理学の分野で広く使われています。
例えば、下の図に示されているように、外力Pによって引っ張られている部材を考えてみましょう。
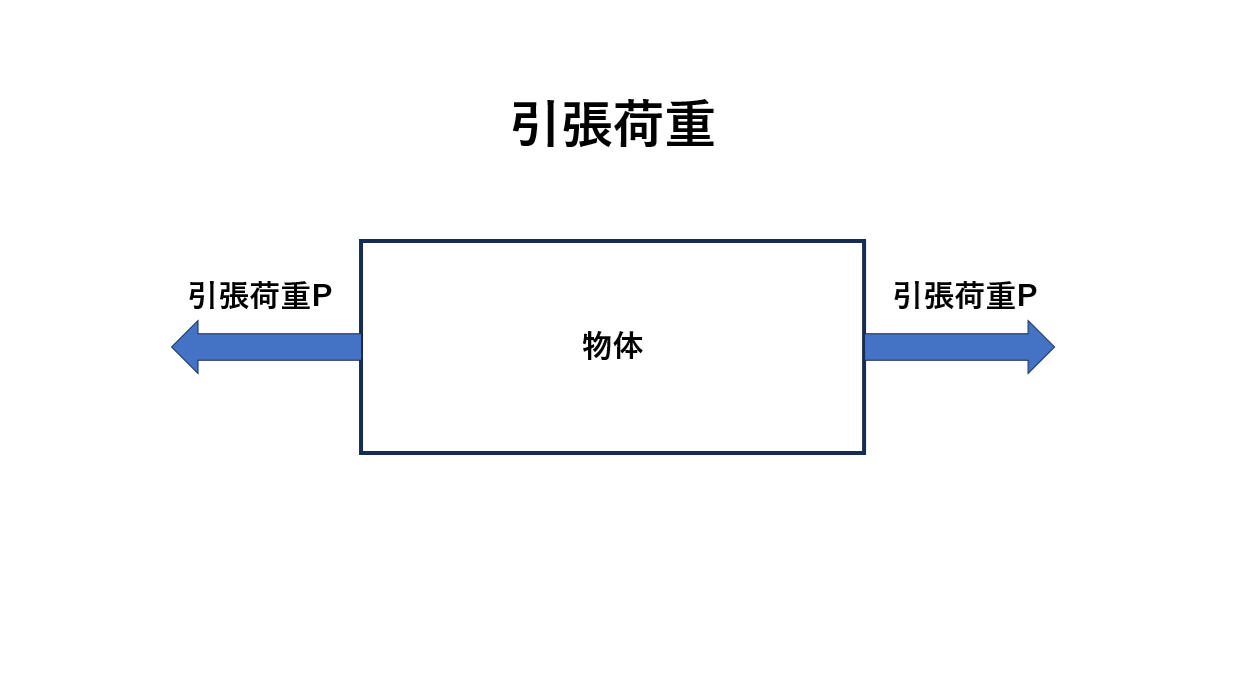
この部材に外力(引張荷重)が加わった場合、もしも部材に抵抗する力が全く存在しなければ、部材は大きく伸びてしまい、形状を保つことができないでしょう。
しかし、実際に部材は形状を維持しています。これは部材内部で外力による変形に抵抗する力、すなわち外力に抵抗する(応じる)力が働いているのです。
この変形に抵抗する力、外力に応じる力の事を応力(または内力)といいます。
応力の公式
部材に軸方向の荷重がかかると、その荷重を受ける断面には応力が発生します。
例えば、ある丸棒の断面積をA、軸荷重をPとすると、断面に生じる応力σ(シグマ)は次の式で表されます。
$$σ=\frac{P}{A}$$
σ:応力(MPa)
P:軸荷重(N)
A:断面積(mm2)
この式は、丸棒の端面にかかる荷重(P)をその断面の面積(mm2)で割ることで、その断面に生じる応力を求めるものです。
例えば、ある棒の断面積が20mm2でそこに100 Nの力が加わると、応力は次のように計算できます。
$$ σ =\frac{P(N)}{A(mm^2)}=\frac{100N}{20mm^2}=5N/mm^2$$
応力の単位
応力は力(N)を面積(mm2)で割ったものなので、単位は N/mm2 もしくはMPaで表されます。
材料力学では、応力はかなり大きな値となってしまうので、MPa(=106 Pa) の方をよく使います。
建築物や機械の設計を行う際には、まず最初に応力を計算することが不可欠です。これは外部から加わる力や荷重が構造物や部品にどのように影響を与えるかを評価し、その応力の大きさが設計基準に適合しているかどうかを確認するためです。
応力が基準値を超えると構造物や機械の安全性や耐久性に問題が生じる可能性があるため、設計者はこれを慎重に検討する必要があります。
応力と応力度の違い
応力と応力度の違いをそれぞれまとめると以下のようになります。
応力(Stress)
- 定義::物体の内部に作用する力のことです。外部からの力が物体に加わったとき、その外力によって生じる変形やひずみの度合いを表す物理量です。
- 単位::パスカル(Pa)やメガパスカル(MPa)、またはニュートン毎平方ミリメートル(N/mm²)で表記されます。
応力度(Strength)
- 定義: 応力度は、単位面積当たりに作用する応力のことで、材料や部品がどの程度の応力に耐えられるかを表しています。つまり、材料が破壊や変形することなくどこまでなら耐えられるのかに着目しているのが応力度です。
- 単位::応力と同じく、パスカル(Pa)やメガパスカル(MPa)で表記されます。
応力と応力度の違いについて考える際には、「応力」という言葉が使われる分野によってその意味が少し異なることに注意が必要です。
例えば、学問の分野では、物理量である応力をそのまま「力」として扱うことが一般的ですが、機械設計や建築の分野では、この力を「応力」と呼びます。
さらに、機械工学で「応力」として扱われる物理量が、建築土木の分野では「応力度」と称されることもあります。
このように同じ「応力」という用語でも、分野によって異なる意味を持つ場合があるため、自分が参考にしている教科書や文献がどの分野に属しているのかを意識しながら読み進めることが重要です。
【ポイント】応力と応力度の微妙な違いのとらえ方
論文や皆さんがこれから計算しようとしているのは「応力度」になります。理由はシンプルで、どこにどんな力がかかっているのかを正確に知りたいから単位面積当たりに作用する応力をこれからいっぱい計算していくことになります。一方、口頭で説明する際や高校レベルの内容では「応力」という傾向があります。
すごく細かな内容ですが、この2つの違いをおさえて材力の勉強をするとより理解が深まりますので、ぜひこの機会に違いを覚えておきましょう。
応力と圧力の違い
先ほどまでは、応力について触れてきましたが、ここで「応力は単位面積あたりの力を示すけど、圧力とは違うの?」と疑問に思われる方もいるかもしれません。
実は応力と圧力は単位が同じです。
では応力と圧力の違いがどこにあるのかというと、それは力が発生する場所にあります。
具体的には、物体の表面にかかる単位面積あたりの力を圧力と呼び、一方で物体の内部に生じる単位面積あたりの力を応力と呼びます。
つまり圧力は外部からの作用によって物体の表面にかかる力を示すのに対し、応力は物体内部で発生する力の状態を表すものです。
応力の種類
応力には、大きく分けると4つの種類があります。
垂直応力(引張応力と圧縮応力)
垂直応力は主に、引張応力(引っ張る力)と圧縮応力(押し込む力)の2種類に分類されます。
引張応力と圧縮応力の公式は、
$$σ=\frac{P}{A}$$
で表します。
引張応力
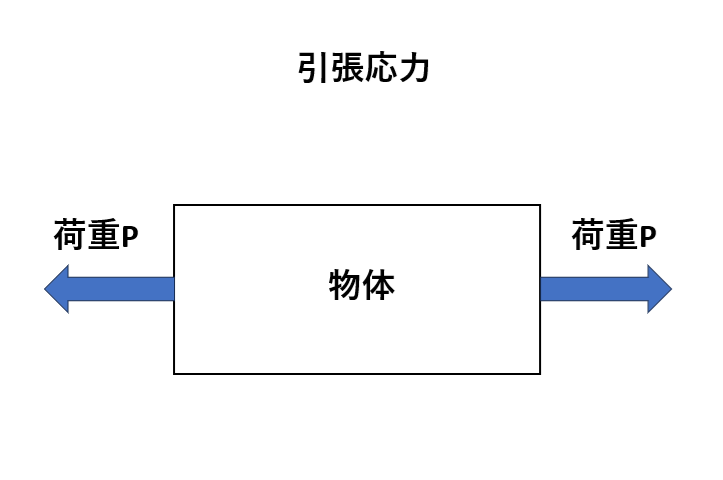
引張荷重は物体が引っ張られることによって発生する力です。引張荷重がかかると物体の内部で分子間の距離が増加し、材料が引き延ばされます。
引張荷重は主に鋼や複合繊維などの材料で強い抵抗を示す特徴があります。材料の引張強度は、引張荷重に対してどれほど耐えられるかを示す指標となります。
圧縮応力
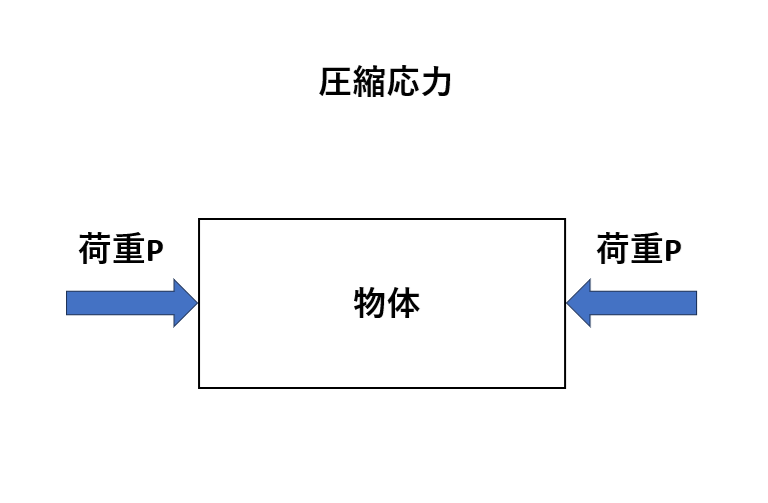
圧縮荷重は物体が押しつぶされることによって発生する力です。この力は物体の長さを短くする方向に作用します。圧縮荷重がかかると物体の内部で分子間の距離が減少し、材料が圧縮されます。
一般的にコンクリートや陶器などが圧縮強度が高い材料として挙げられますが、鋼やアルミニウムも圧縮に対しても比較的優れた性能を持っています。
せん断応力
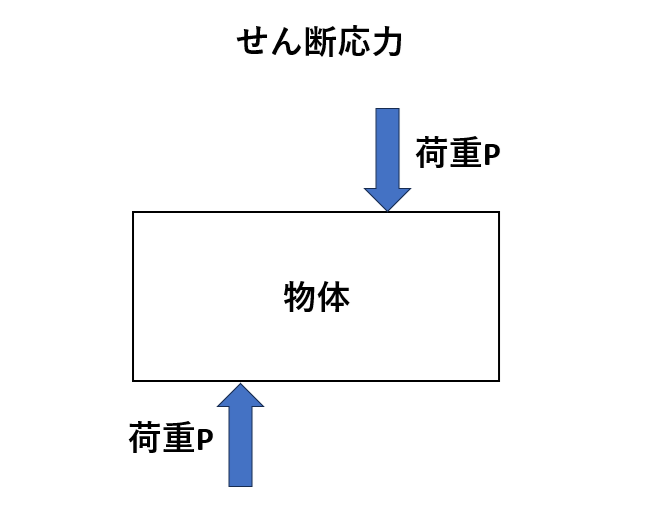
せん断応力とは、物体を横方向にずらす際に発生する力のことで、単位面積あたりにかかるせん断力のことを指しています。
物体を互い違いにずらす外力をせん断荷重と呼び、それによって物体内部に発生する力をせん断力と言います。別の言い方をすると、せん断荷重は横方向の力、そしてせん断力は内部せん断応力と表現することができます。
記号はτ(タウ)で表されます。式で表すとこのようになります。
$$τ=\frac{P}{A}$$
τ:せん断応力(MPaまたはN/mm2)
A:断面積(mm2)
P:せん断応力(N)
せん断応力が材料が耐えられる限界を超えると、その材料は壊れてしまいます。これを「せん断破壊」と呼びます。
曲げ応力
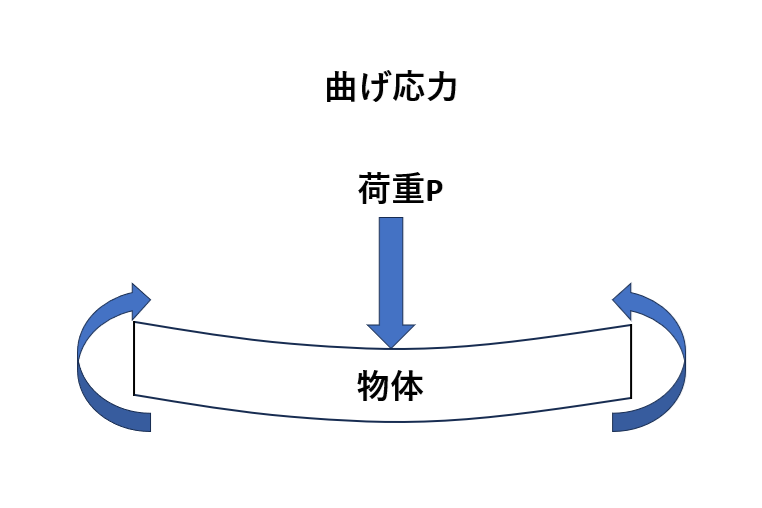
曲げ応力とは、曲げモーメントが材料に作用することで内部に生じる垂直方向の応力を指します。
曲げ応力の公式は以下のように表します。
$$σ=\frac{M}{Z}$$
σ:曲げ応力(MPa)
M:曲げモーメント(Nmm)
Z:断面係数(mm3)
材料に曲げモーメントを加えると、上部には圧縮応力が、下部には引張応力が生じます。
また、伸びや縮みが発生しない面を「中立面」と呼び、中立面と断面が交差する軸を「中立軸」といいます。
曲げ応力は、「曲げモーメント」と「中立面からの距離」を用いて、断面二次モーメントで割ることで表されます。
外力として表記されるPとFの違いについて
例えば、下図のような部材に外力Pが作用しているとします。
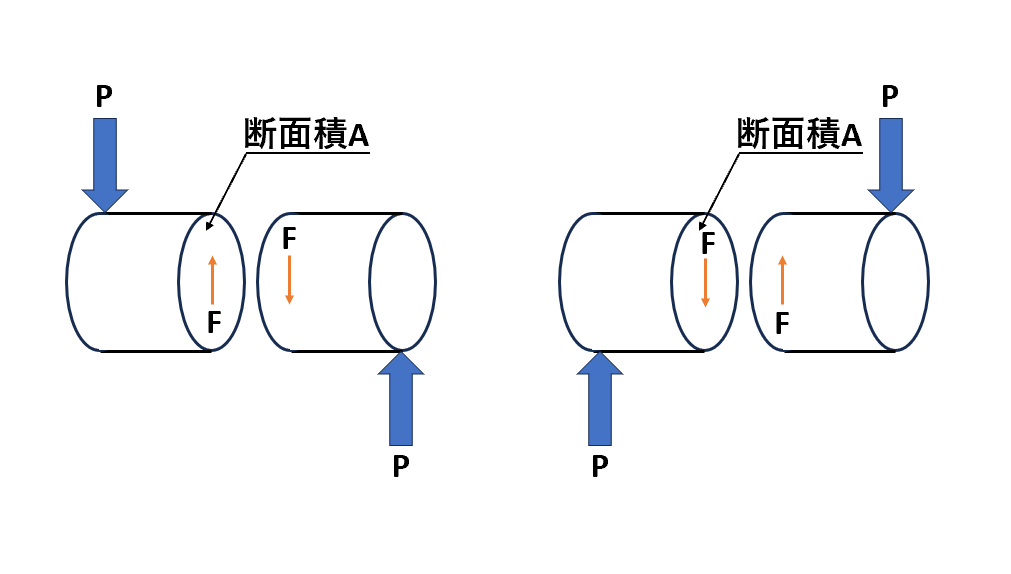
仮想断面内に発生している内力はFとおき、これを式で表すと、
$$τ=\frac{F}{A}$$
となります。(せん断応力の公式)
このように教科書によっては、応力をPと表す場合とFと表す場合がありますが、基本的に同じ物理的意味を持ちます。
この場合のせん断応力では、どちらもある物体の断面で平行に作用する外力を指していて、記号の選択は主に文献や分野ごとの慣習によるものです。
基本的には同じ物理的意味を持ち合わせているPとFですが、特徴をまとめると以下のような違いがあります。
PはLoad(荷重)としての記号
- Pは、「荷重」を意味する「Load」に由来します。
- 主に構造力学や材料力学の分野で使われることが多いです。
- 特定の構造や部材に加わる「全体的な外力」を表現する際に適しています。
FはForce(力)としての記号
- Fは、力を表す「Force」の頭文字に由来します。
- 力学や物理学の分野で広く用いられる一般的な記号です。
- 力のベクトル的な性質を強調する際や、局所的な力(例えば断面のせん断力)を扱う場合によく使われます。
軸荷重(軸力)について
軸荷重とは、物体の軸方向に沿って加わる力のことです。たとえば、柱にかかる重さや、引っ張られるロープの力、棒や柱に対してその長さに沿って引っ張ったり押し込んだりする力が軸荷重です。
この力は物体が圧縮されるときと引っ張られるときに発生します。例えば、柱やロッドなどの構造物では、上からの荷重に対して垂直に力が作用しますが、ここで働いている力が軸力です。
参考までに下記に軸荷重についての定義が書かれていたページを見つけましたので、そちらもご確認いただいてもらうとより理解が深まると思います。
軸(方向)荷重
物体に作用する荷重の方向が物体の幾何学的対称軸や中心軸の方向に一致するとき,その荷重を軸(方向)荷重という.また,物体内部に生ずる内力の方向がこれらの軸の方向に一致するとき,軸方向力あるいは軸力という.
引用:機械工学事典
私たちの身の回りのもので軸荷重は体験できる?
軸荷重は製品やモノがどんな構造になっているか、というのを意識して見てみると、実はいろんなところに軸荷重があるんだなというのを発見できると思います。
例えば、あなたが長いストローを持っているとしましょう。ストローの端を押すと、ストロー全体が圧縮させようとする方向に力が働きだします。このときのストローの内部にかかっている力が「軸荷重」です。逆に、ストローの両端を引っ張るとストローが伸びますが、これも軸力が働いている状態といえます。
ほかにも軸荷重を体験できる例をいくつか挙げてみました。
- ベンチ
-
公園やカフェのベンチに座ると、あなたの体重がベンチの脚にかかります。このときのベンチの脚にかかる力が軸荷重です。脚が縦の方向に力を受けるため、軸力が発生していますね。
- スーツケース
-
スーツケースを持ち上げると、その取っ手やハンドル部分に軸荷重がかかります。特に持ち上げるときの力が取っ手に集中します。
- 自転車のフレーム
-
自転車に乗ると体重がフレームにかかります。この力は、自転車のフレームの各部に軸荷重として伝わります。特に、ハンドルやサドルの部分で顕著です。
このように私たちの日常生活の中には、軸荷重が働いている構造物や製品がたくさん存在しています。ストローの例からもわかるように物体の形状や材質によって、どのように力が伝わり、どのように力が物体を支持しているのかを意識することで、周囲の物を新たな視点で見ることができます。
軸荷重のイメージがつかめたところで次の項目では、実際に応力と軸荷重を扱った問題を計算していきたいと思います。
計算問題
例題1
50Nの引張荷重が作用する断面積20mm2 の丸棒材料に発生する応力を求めなさい。

ポイント
断面積をmm2、荷重をNで応力の公式に代入してあげると求まります。
例題1の解答
応力の式
$$σ=\frac{P}{A}$$
にそれぞれ数値を代入。
$$σ=\frac{P}{A}=\frac{50}{20}=2.50MPa$$
解:5MPa
例題2
20kNの圧縮荷重が作用する直径30mmの丸棒に発生する応力を求めなさい。
ポイント
円の断面積を直径dで表した形に式変形します。その後例題1で出てきた応力の式に荷重を代入します。
例題2の解答
円の断面積の公式
$$A=\frac{πd^2}{4}$$
応力の式
$$σ=\frac{P}{A}$$
応力の式に円の断面積の公式を当てはめるとこうなります。
$$σ=\frac{P}{A}$$
$$σ=\frac{\frac{P}{1}}{\frac{πd^2}{4}}=\frac{4P}{πd^2}$$
そしてそれぞれの数値をあてはめます。
$$σ=\frac{4P}{πd^2}$$
$$σ=\frac{4×20×10^3}{π×30^2}=28.31MPa$$
※Pの20×10^3は10「k」Nなのでこのように表記します。
解:28.31MPa
まとめ
今回の計算で重要な点は、応力と軸重の関係を正確に理解することです。
特に、応力が材料の強度にどのように影響するのかを把握することが大切です。
材料力学はこの応力の式を使った計算がとても多いです。
どんな場所にどのくらいの力が働いているのかを常に頭の中で想像することで、計算式の意味や結果の解釈がしやすくなると思うので、是非この機会にそのスキルを磨いてください!
