軸荷重の計算方法でお悩みではありませんか?
本記事では、異なる2つの材料に軸方向の荷重が作用する際にどのような計算を行えばよいのか、具体的な事例を交えながらわかりやすく解説しています。
構造物が荷重にさらされる場面は日常の部品から建築分野まで多岐にわたりますが、その中でも「軸荷重の組み合わせ問題」は材料力学の計算問題としてよく登場するテーマです。
この記事を読むことで、材料に軸荷重が作用した際の計算方法が習得でき、安全性や耐久性の評価に必要な知識をしっかりと身に付けることができるでしょう。また、異なる材料を組み合わせた場合の縦弾性係数や断面積が材料にどう影響を及ぼすのかについても考察しているので、実務や学習の場で役立つような内容となっています。
ぜひ最後までお読みいただき、軸荷重の計算をマスターしましょう。
軸荷重とは?
はじめに軸荷重についてです。
軸荷重とは物体にかかる力のうち、物体の軸に沿った方向にかかる荷重のことを指します。
簡単に言うと、部品や材料の軸に沿って発生する荷重のことを言います。。
そして軸荷重には、基本的に引張応力と圧縮応力の2種類があります。
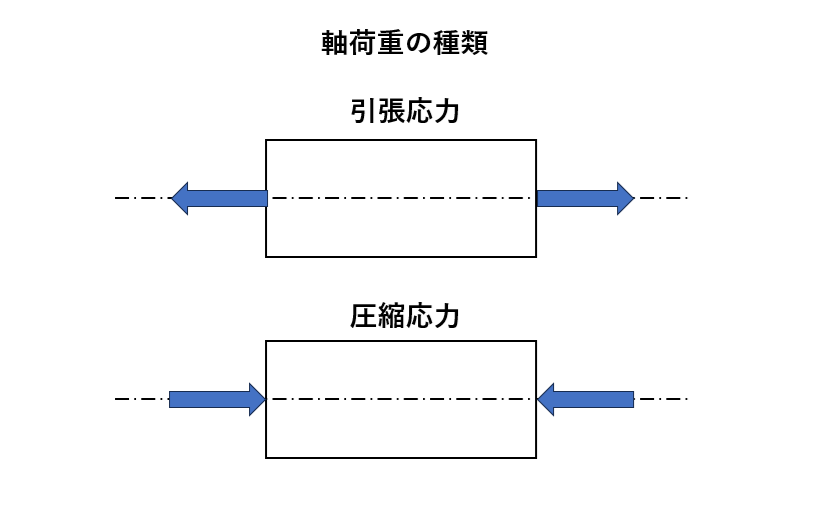
材料力学において、軸荷重は以下のような場面でよく出てきます。
- 構造物の設計
柱や梁などの構造物において、どれだけの荷重に耐えられるかを評価するために軸荷重が用いられます。特に、圧縮や引張に対する強度を確認する際によく出てきます。
- 応力解析
軸荷重がかかる部材では、材料内部に生じる応力(引張応力や圧縮応力)を計算する必要があります。外部から応力が加わったとき、どのくらいまでだったら材料が破損しないかをFEM解析などを使って判断していきます。
軸力と軸荷重の違い
軸荷重と似た言葉で、「軸力」という単語があります。
引張荷重や圧縮荷重のように、力の作用線が材料の軸線(中心線)に沿って働くものを軸荷重といいます。
一方で、材料の力の作用線に垂直な仮想断面に発生する内力を軸力と呼びます。
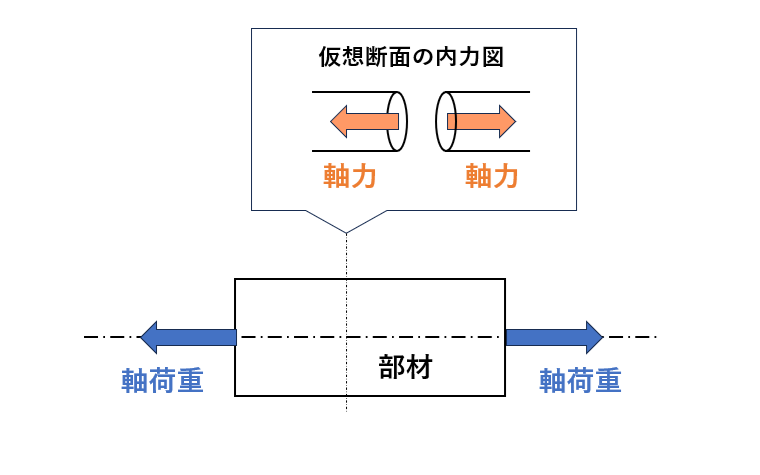
上記のような観点から、軸荷重とは材料の軸方向に働く外部からの力のことを指しており、軸力とはその軸方向に発生する材料内部の力を表していることが分かります。
アキシアル荷重と軸荷重
ベアリング製品のカタログなどによく出てくる単語で、「アキシアル荷重」というものがあります。
アキシアル荷重は、軸と同一方向にかかる荷重のことを呼びます。
実は、このアキシアル荷重も単語が違うだけで、軸荷重と意味は一緒です。
このアキシアルは英語で書くとaxial(軸)となり、ベアリング製品では荷重の影響が製品性能を大きく左右してしまうことからあえてこう呼んでいるのかもしれません。
使われる場面の違い
アキシアル荷重という名称は英語の「axial load」がベースになっており、ベアリング部品や製品カタログ、メーカー仕様書などでよく用いられます。一方、日本語の教材や建築・土木などの分野では「軸荷重」という言葉が一般的に使われることが多いです。
いずれの呼び方も「軸方向に作用する力」という点では同義ですが、
- アキシアル荷重・・・英語圏や海外文献、ベアリング関連カタログで使われることが多い
- 軸荷重・・・材料力学や建築分野など国内の文献や学術書で用いられることが多い
という特徴があり、こうした背景から文献によって表現が異なる場合があります。しかし、指している内容は同じという点を理解しておくと覚えやすいでしょう。
ちなみに垂直方向にかかる荷重はラジアル荷重と呼んでいます。材料力学の世界ではよく垂直応力と言ったりしている荷重のことです。
また、ベアリングのカタログでは、主にラジアル荷重を受ける軸受をラジアル軸受、アキシアル荷重を受ける軸受をスラスト軸受と言ったりします。
2つの異なる材料に軸荷重が作用した場合の考え方
ここでは、以下のような2つの円筒部品に10kNの圧縮荷重が作用している場合を考えていきます。
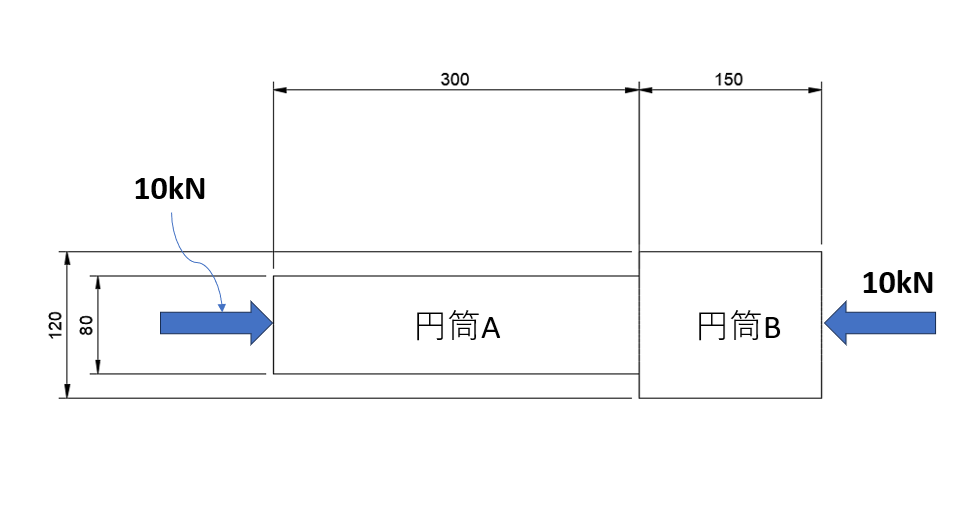
複数の異なる材料が組み合わされ、そこに軸荷重(今回は圧縮荷重)が発生している場合、以下の内容をおさえておく必要があります。
円筒Aと円筒Bがそれぞれ異なる材料を使用していたとき、円筒Aと円筒Bでは縦弾性係数が異なるため、同じ荷重がかかっても変形量が異なります。
よって、各円筒がどれだけ変形するかを個別に計算し、それを合算する必要があります。
円筒AとBの縦弾性係数は、
$$縦弾性係数E=\frac{σ}{ε}$$
より求めることができます。
異なる材料が2つある場合、両端にかかる荷重は同じ10kNでもそれぞれの円筒で発生する変形量(λ)が異なるため、縦弾性係数と同様に各円筒での圧縮量を別々に計算します。
そして、それらの変形量を合計して全体の圧縮量を求める、という計算方法で進めていきます。
変形量の算出については、
$$λ=λ_{1}+λ_{2}$$
と式を立て、λ1=材料A、λ2=材料Bとおいて個別に計算すると最終的に全体の変形量が決まります。
材料が1種類のときは均等に荷重がかかりますが、複数の異なる材料が組み合わされていた場合、縦弾性係数や断面積の違いによって荷重が異なる割合で分布します。
ここの内容をおさえたうえで、次は実際に問題を解いてみましょう。
計算問題
例題1
直径80mm、長さ300mm、縦弾性係数200GPaの円筒Aと、直径120mm、長さ150mm、縦弾性係数100GPaの円筒Bが中心軸を合わせて組み合わされ、その両端に10kNの圧縮荷重が作用している。全体の圧縮量を求めなさい。
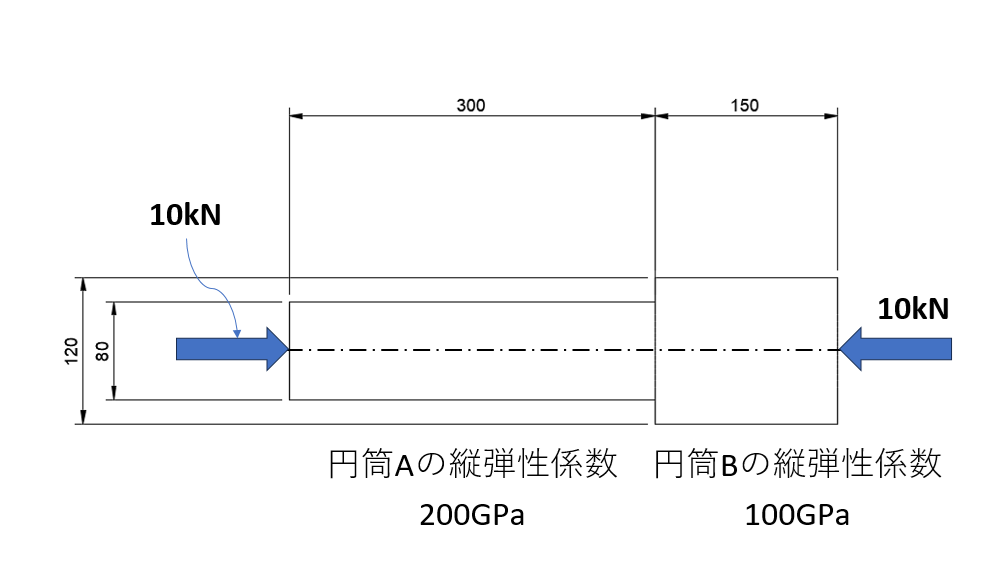
ポイント
縦弾性係数の式
$$E=\frac{Pl}{Aλ}$$
をλ=~~~という形に式変形し、その式から全体の圧縮量を求める。
なぜ、縦弾性係数の式が上記のようになるのかについては、
$$①応力の式σ=\frac{P}{A}$$
$$②縦ひずみの式ε=\frac{λ}{l}$$
の二つの式を
$$③縦弾性係数の式E=\frac{σ}{ε}$$
の式にそれぞれ代入してあげると求まります。ココの導出についての内容は以下の記事でまとめています。

例題1の解答
円筒Aの圧縮量をλ1、円筒Bの圧縮量をλ2として最初にそれぞれの圧縮量を計算し、その後全体の圧縮量を求める。
①円筒Aの圧縮量
$$λ_{1}=\frac{Pl_{1}}{A_{1}E_{1}}$$
$$=\frac{\frac{Pl_{1}}{1}}{\frac{πd_{1}^2E_{1}}{4}}$$
$$=\frac{4Pl_{1}}{πd_{1}^2E_{1}}$$
$$=\frac{4×10×10^3×300}{π×80^2×200×10^3}$$
$$=0.005968$$
λ1=0.005968mm
②円筒Bの圧縮量
$$λ_{2}=\frac{Pl_{2}}{A_{2}E_{2}}$$
$$=\frac{\frac{Pl_{2}}{1}}{\frac{πd_{2}^2E_{2}}{4}}$$
$$=\frac{4Pl_{2}}{πd_{2}^2E_{2}}$$
$$=\frac{4×10×10^3×150}{π×120^2×100×10^3}$$
$$=0.001326$$
λ2=0.001326mm
③全体の圧縮量を求める
$$λ=λ_{1}+λ_{2}$$
$$=0.005968+0.001326=0.007294mm$$
$$=7.29×10^{-3}mm$$
解:全体の伸びλ=7.29×10-3mm
例題2
外径12mm、ねじ山のピッチが1.75mmのボルトとナットで部材Aと部材Bを45mmの厚さで締め付けている。このときボルトの軸部に180MPaの引張応力が発生している。ここでナットを右回しに15度締め付けて増し締めした。ねじの有効断面積84.3mm2、縦弾性係数を206GPaとしたときのボルトの軸部に発生する引張応力の増加分を求めなさい。
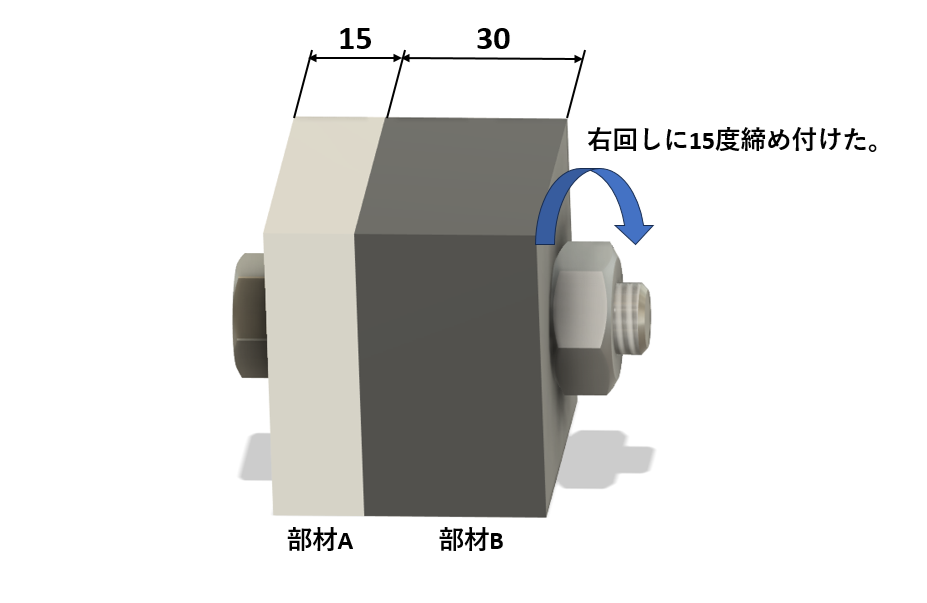
ポイント
変形はボルトだけに発生するものと考え、ナットを10°回転させた時の変位と同じ長さだけボルトがボルトが伸ばされる、と考える。
この問題は、ボルトとナットの締め付けによる引張応力の変化を求めるものです。
ナットを回しても実際にはボルトの軸部のみが伸びるという考え方を指しています。
ナットを回すことでボルトが引っ張られ、その結果ボルトに引張応力が生じます。
このとき、ナットの回転角度からボルトの伸びを求めることができます。
そしてボルトの伸び(λ)は以下のような式が成り立ち、この式よりボルトの変位量を求めることができます。
$$ボルトを回転した時の変位$$
$$=\frac{ピッチ[mm]×ボルトを回転させた角度[°]}{360°}$$
例題2の解答
縦弾性係数Eの公式
$$E=\frac{Pl}{Aλ}$$
からσ=~~~の式に整理し、ボルトに発生している応力を求める。
$$E=\frac{Pl}{Aλ}$$
$$E×\frac{λ}{l}$$
$$=\frac{P\cancel{l}}{A\cancel{λ}}×\frac{\cancel{λ}}{\cancel{l}}$$
$$E\frac{λ}{l}=\frac{P}{A}$$
ここで
$$\frac{P}{A}$$
はσに置き換えられるので、このように表します。
$$σ=E\frac{λ}{l}$$
$$σ=λ\frac{E}{l}$$
この式を用いてボルトに発生している応力を求めます。ここでλは、
$$ボルトを回転した時の変位$$
$$=\frac{ピッチ[mm]×ボルトを回転させた角度[°]}{360°}$$
から求めことができますので、問題文に出てきた数値をここの関係式にあてはめます。
$$σ=λ\frac{E}{l}$$
$$σ=\frac{1.75×10}{360}×\frac{206×10^3}{45}$$
$$=222.53MPa$$
解:222.53MPa増加する。
まとめ
今回の記事を通じて、「軸荷重の組み合わせ問題」に関する基礎的な知識から計算方法を学んでいただけたのではないでしょうか。
異なる材料が組み合わさって軸荷重が発生した場合の計算方法や、縦弾性係数を考慮した変形量の求め方は、実務や学問の分野で役立つはずです。
ぜひ、今回のポイントをおさえてもらえればと思います。
今後、軸荷重以外の荷重や複雑な力学条件を含む問題に取り組む際にも、本記事で解説した内容が基礎となります。ぜひ繰り返し学習し、実践的に応用してみてください。
本記事が皆様の学習や実務に少しでもお役に立てば幸いです。
最後までお読みいただきありがとうございました。
