今回は薄肉円筒器と球体容器に発生する応力について説明していきたいと思います。
薄肉円筒器と球体容器は圧力容器として使用されており、それぞれ独自の応力特性を持っています。
これらの構造体に圧力(内圧)がかかると、ほかの構造物とは異なる応力が発生します。
この記事では薄肉円筒器と球体容器の応力の違いや計算方法について詳しく解説していきます。
これにより材料力学の理解を深め、実際の設計や解析に役立てていただければなと思います。
薄肉円筒とは
最初に薄肉円筒とは、板厚が内径の約12%以下、または外径の約10%以下の円筒のことをいいます。
この円筒形状は、主にガスなどの流体圧力を封じ込めるための容器として使用されます。
そして、薄肉円筒の内部に圧力が存在する場合、主に2つの応力が発生します。
- 円周方向の応力(σr):円筒の円周方向に作用する応力です。フープ応力と呼ばれる応力です。
- 軸方向応力(σz):円筒の縦方向に作用する応力で、計算するとフープ応力の半分の値になります。
薄肉円筒の特徴
薄肉円筒は、内圧や外圧に対して耐えられるように設計されていますが、板厚が薄いため構造的な強度が求められます。
用途
薄肉円筒はガスタンクやパイプライン、圧力容器など、流体を安全に運搬または保管するための容器として広く利用されています。
また、航空機や自動車の部品、化学プラントの装置など、高い圧力や温度にさらされる環境でも使用されることがあります。
選定方法
一般的には鋼やアルミニウム、プラスチックなどの軽量で強度のある材料が使用されます。使用する材料によって、円筒の耐久性や耐腐食性が変わるため、用途に応じた材料選びが重要になります。
製造方法
成形方法にはロール成形、押出成形、溶接などがあり、これらの工程により円筒の精度や仕上がりが大きく影響します。
特に溶接技術は薄肉の特性を活かしつつ、強度を確保するために重要な要素です。
薄肉円筒は板厚が薄いことで材料の使用量を減らし、コスト効率を高めることができるメリットがあります。
ほかにも、成形や加工がほかの形状よりも容易なので生産効率が上がったり、冷却や加熱が効率的に行えるようにするためにこのような形状を採用する場合があったりします。
フープ応力
薄肉円筒容器と密接に関わりがあるのが、フープ応力という力です。
フープ応力とは、密封された円筒容器に円周方向に内部圧力がかかった応力のことをいいます。円周応力と呼ぶこともあります。
フープ応力を考える際には、円筒容器の軸方向(縦方向)に働く軸方向の応力と、円周方向に働く応力の二つの成分に分けて分析することが重要です。
この2つの計算から、容器の強度や安全性を正確に評価することができます。
例えば、内径D、内側の長さl、厚さtを持つ薄肉円筒に封入された内圧pの流体があったとき、内圧pは円筒の内壁に対して等しく圧力をかけます。
そしてこの圧力は、内壁に対して外向きの力を発生させます。このとき、圧力pの流体は軸と垂直な方向に内壁を引き離そうとする力Prを与え、 薄肉円筒容器内部には引張応力σrが発生します。
この応力σrがフープ応力であり、フープ応力は内圧の大きさ、円筒の内径、厚さに依存します。
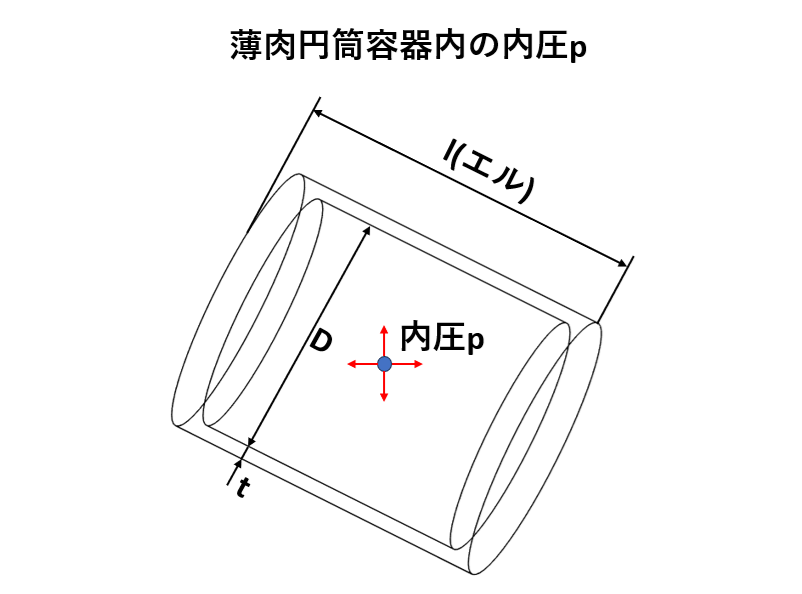
フープ応力の式は下記のように表します。
$$フープ応力σ_{r}=\frac{P_{r}}{A}$$
ここで、
$$両側の肉厚断面積A=2lt$$
$$長方形の断面積(Dl)と内圧(p)の積Pr=pDl$$
をそれぞれ代入すると、
$$フープ応力σ_{r}=\frac{pD\cancel{l}}{2\cancel{l}t}=\frac{pD}{2t} ・・・(1)$$
と求めることができます。
この式(1)は円筒の円周方向に作用する圧力を考慮したもので、圧力が大きくなるほど円周方向の応力も大きくなることを示しています。
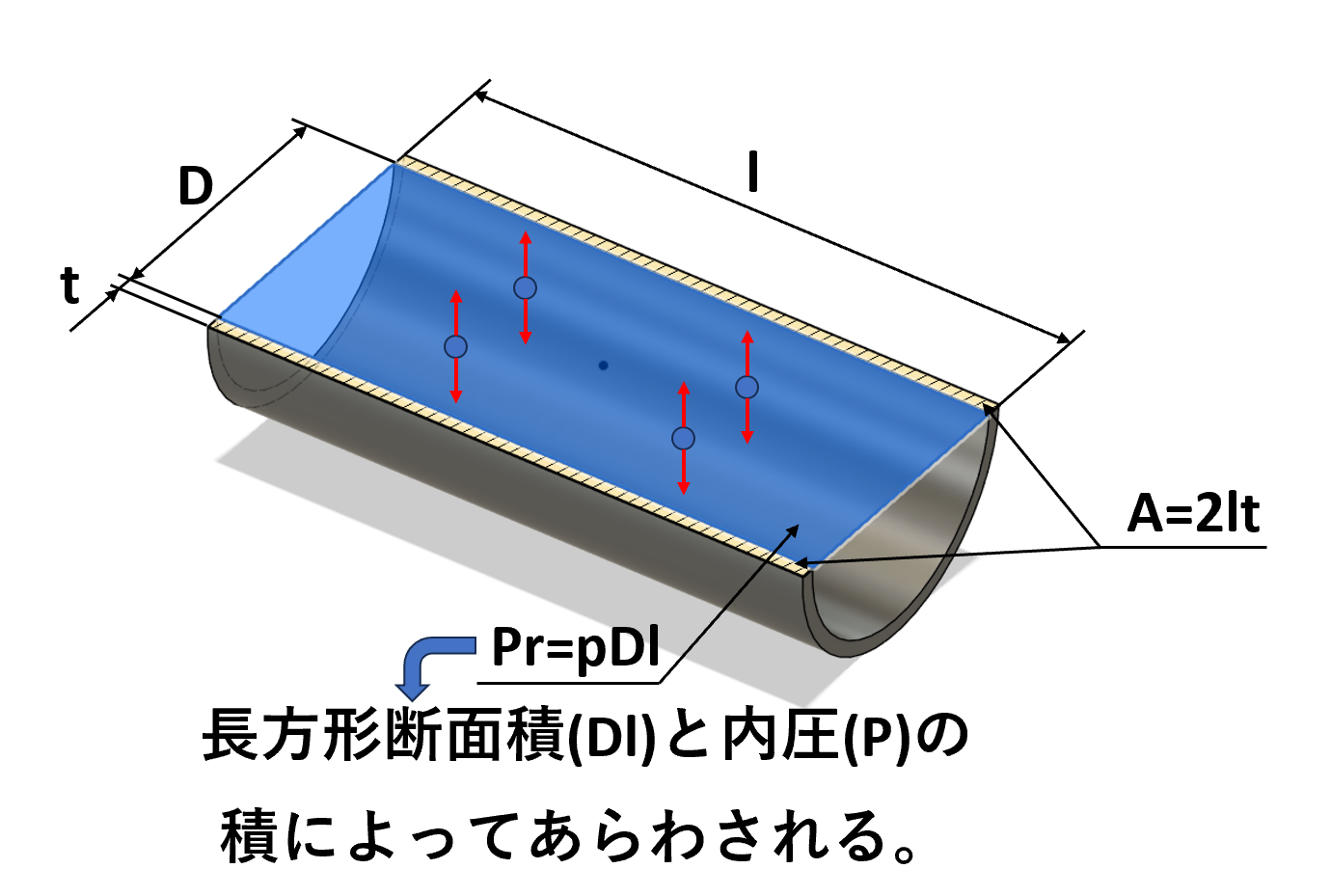
フープ応力が発生することのメリット
フープ応力が発生することには、以下のようなメリットがあります。
- 構造の強化
フープ応力は円筒容器の壁に均等に分布するため、内部圧力に対して強度を増す効果があります。これにより、容器が破損しにくくなります。 - 圧力保持能力の向上
フープ応力によって容器は内部の流体やガスの圧力を効率的に保持できるため、特に高圧の環境でも安全性が向上します。 - 均一な応力分布
フープ応力は円周方向に均一に分布するため、局所的な応力集中を避けることができ、全体的な構造の耐久性が向上します。 - 長寿命化
フープ応力が適切に設計されている場合、円筒容器の寿命が延び、メンテナンスや交換の頻度を減少させることができます。
軸方向の応力
今度は容器内部の軸方向の応力について考えます。
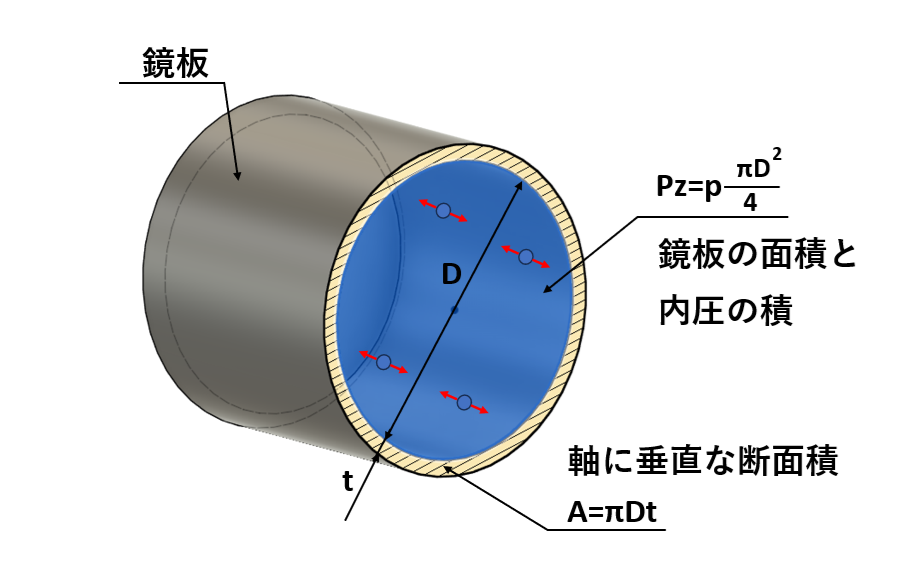
例えば以下の図のような容器に内部圧力が発生していた場合、容器の軸方向には両端の鏡板にかかる力Pzが発生します。
この力Pzの大きさは内圧Pと鏡板の直径Dをかけ合わせた面積の積となり、材料はこの力を軸に垂直な断面、つまりPzは直径Dの円周の長さπDと幅tの積で受け止めます。
よって、鏡板にかかる力Pzを式で表すと以下のようになります。
$$両端の鏡板にかかる力P_{z}=\frac{pπD^{2}}{4} ・・・(2)$$
p:内圧
πD2/4:鏡板の断面積
軸に垂直な断面積については、材料の厚みtと断面積、円周率πを掛け合わせて、
$$A=πDt ・・・(3)$$
となります。
よって、軸方向の応力は式(2)と式(3)を使って求めると、
$$軸方向の応力σ_{z}=\frac{P_{z}}{A}$$
$$=\frac{\frac{pπD^{2}}{4}}{\frac{πDt}{1}}$$
$$=\frac{p\cancel{π}D^{\cancel{2}}}{4\cancel{π}\cancel{D}t}$$
$$=\frac{pD}{4t} ・・・(4)$$
となります。
この式は、円筒の縦方向に作用する応力を示しており、フープ応力の約半分の値をとります。フープ応力の約半分の値になる理由は、円筒の縦方向には圧力が直接作用しないため、応力が小さくなります。
フープ応力と軸方向の応力の使い分け
フープ応力(σr)は最も大きい応力になるため、薄肉円筒関係の材料の強度を評価する際にはこの応力を基に計算することが重要になります。
例えば、薄肉円筒容器の厚さ計算を行う際フープ応力を用いることで、容器が安全に圧力を保持できるかの評価ができます。容器が内圧に耐えられるかどうかを評価するためには、この応力を基に厚さを求めることが必要です。
そして、フープ応力が安全基準を満たす場合、容器は安全であると判断できるのです。
一方で、軸方向応力はフープ応力の半分であり直接的な圧力の影響を受けにくいことから、薄肉円筒の設計においてはあまり考慮されない傾向があります。
球体容器の応力
内径D、厚さtの球体に内圧pの流体を密閉すると、球体を二つに引き離そうとする力Pが生じます。
この力Pの大きさは、内圧pと直径Dの円の面積の積で表されます。
一方、この力は直径Dの半球断面の円周の長さπDと厚さtの積で受け止められます。
球体容器の応力も、薄肉方向の軸方向に発生する応力と同様の式で表すことができます。
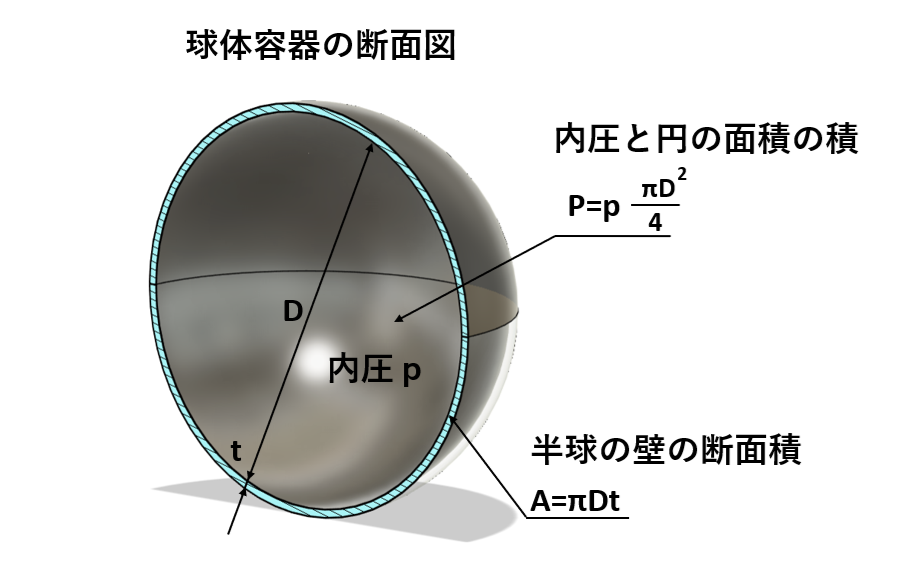
上記の図から、球体容器の応力σは、
$$σ=\frac{P}{A}$$
$$=\frac{\frac{pπD^{2}}{4}}{\frac{πDt}{1}}$$
$$=\frac{p\cancel{π}D^{\cancel{2}}}{4\cancel{π}\cancel{D}t}$$
$$=\frac{pD}{4t} ・・・(5)$$
となります。
外圧と内圧の違いについて
ここでは外圧と内圧の違いについて解説します。
外圧と内圧は、構造物や材料に作用する圧力が異なります。
外圧は材料や構造物の外側から作用する圧力であり周囲の環境(例えば大気圧や水圧)によって生じます。外圧は主に圧縮応力を引き起こし、構造物の安定性に影響を与えます。例えば、地下に埋設されたパイプラインや水中にあるタンクは、周囲の土壌や水の外圧を受けています。
一方、内圧は、材料や構造物の内部から作用する圧力で、内部に封じ込められた流体(ガスや液体)が加圧されることによって生じます。内圧は引張応力を引き起こし、構造物の壁が膨張する原因となります。圧力タンクやガスタンク、アキュームレータ(蓄圧器)の内部では、この内圧が常に発生しています。
そして外圧と内圧の両者は異なる方向から力が作用していることから、それぞれの力が構造物に与える影響を相殺し合うこともあります。
このため、時には設計時に外圧と内圧のバランスを考慮し、材料の強度や構造の安定性を確保する必要があります。
例えば、圧力タンクは内圧によって壁が膨張し同時に外圧もかかるため、これらの圧力の相互作用を理解することが重要で、適切な設計がなされていない場合だと、過剰な外圧や内圧が構造物に対して危険な状態を引き起こす可能性があります。
次の項目では、フープ応力を扱った問題に移ります。
計算問題
例題1
内径300mmの円筒容器に圧力6MPaの気体を封入した場合、容器の厚さを求めなさい。なお、許容引張応力は40MPaとします。
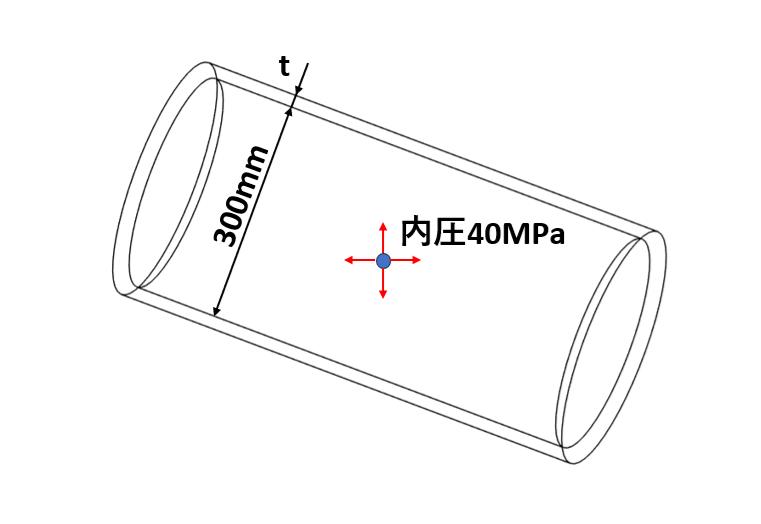
ポイント
フープ応力が大きいので、式(1)の、
$$フープ応力σ_{r}=\frac{pD}{2t}$$
を使って計算します。
例題1の解答
式(1)を使って厚さtを算出。
$$フープ応力σ_{r}=\frac{pD}{2t}$$
$$σ_{r}×\frac{2}{pD}=\frac{\cancel{p}\cancel{D}}{\cancel{2}t}×\frac{\cancel{2}}{\cancel{p}\cancel{D}}$$
$$\frac{2σ_{r}}{pD}=\frac{1}{t}$$
$$t=\frac{pD}{2σ_{r}}=\frac{4×300}{2×40}$$
$$=15.00mm$$
導出した板厚15mmと内径を使って比較します。
$$\frac{t}{D}=\frac{15}{300}×100=5%$$
以上の結果から、板厚が内径の12%以下なので、薄肉円筒のフープ応力の公式が適用できることがわかりました。
解:板厚15mm
例題2
内径500mm、厚さ10mmの薄肉球体容器に完全に封入できる気体の圧力を求めなさい。材料の引張許容応力は30MPaとします。
ポイント
薄肉球体容器なので式(5)の、
$$=\frac{pD}{4t}$$
を使って計算します。
例題2の解答
式(5)の球体容器の応力から内圧pを求めるために、まずは式変形します。
$$σ=\frac{pD}{4t}$$
$$p=\frac{4tσ}{D}$$
この式に数値を当てはめていきます。
$$p=\frac{4tσ}{D}=\frac{4×10×30}{500}=2.40MPa$$
解:安全に封入できる気体の圧力は2.40MPaまで
まとめ
この記事では、薄肉円筒器と球体容器に発生する応力について詳しく解説しました。
薄肉円筒の特性やフープ応力、軸方向の応力の計算方法を把握することで、圧力容器の設計や解析における基礎知識が深まるのではないでしょうか。
今後も材料力学に関する情報をお届けしていきますので、引き続きご覧いただければなと思います。
