このブログ記事では、曲げ応力の基本的な考え方をはじめ、はりに作用する荷重からせん断力図(S.F.D)や曲げモーメント図(B.M.D)を導き出し、最終的に曲げ応力を計算するまでの流れをできるだけ分かりやすく解説していきます。実際に数値を交えた例題を用意し、複数の荷重条件や断面係数の違いがどのように応力に影響を与えるのかも見ていきますので、設計や材料力学に慣れていない方でもイメージがつかみやすい内容になっています。ぜひ、はりの強度設計や応力計算の要点を学んでいただくきっかけとして、ご活用ください。
この記事では、両端支持はりに作用している集中荷重から、S.F.D図(せん断力図)やB.M.D図(曲げモーメント図)を求め、そこから断面係数を用いてはりに発生している曲げ応力を求めていく内容となります。
曲げ応力σとは?
曲げ応力とは、 簡単に言うと材料が曲がった際、内部に発生する引張・圧縮応力のことをいいます。
イメージとしては、はりが下向きにたわむよう曲がった時、はりの上側には圧縮応力がかかり、下側には引張応力がかかり、それぞれの部分で異なる応力が発生します。この応力が大きくなると、材料が折れたり破断したりする原因となるため、構造や部材を設計する際には、どれくらいの大きさの曲げ応力が発生するのか正確に把握することが重要になります。
曲げ応力の公式は、次のような式です。
$$σ=\frac{M}{Z}$$
σ:曲げ応力(MPa)
M:最大曲げモーメント(Nmm)
Z:断面係数(mm3)
曲げ応力についての詳しい内容はこちらで解説しています。

曲げ応力σと曲げモーメントMの関係について
曲げモーメントMは、外部からの荷重などによってはりが曲がろうとする「回転させる力」の大きさを表す量です。一方で、曲げ応力σは、その「回転させる力」が原因で生じる、材料内部の引張・圧縮の度合いを示したものです。
曲げ応力の公式、
$$σ=\frac{M}{Z}$$
で示されるように、はりに発生する曲げ応力σは曲げモーメントMの大きさに比例するので、断面係数Zが大きいほど曲げ応力σは小さくなります。断面係数Zとは、「はり断面の形状が曲げに対してどれほど強いか」を表す指標で、値が大きいほど、同じモーメントでも材料内部に生じる応力が小さくなる、というわけです。
計算問題
例題
次のような縦長部材の両端支持はりに発生する曲げ応力を求めなさい。また、同じ条件下で横長断面ではりを使用した場合の曲げ応力も求めなさい。
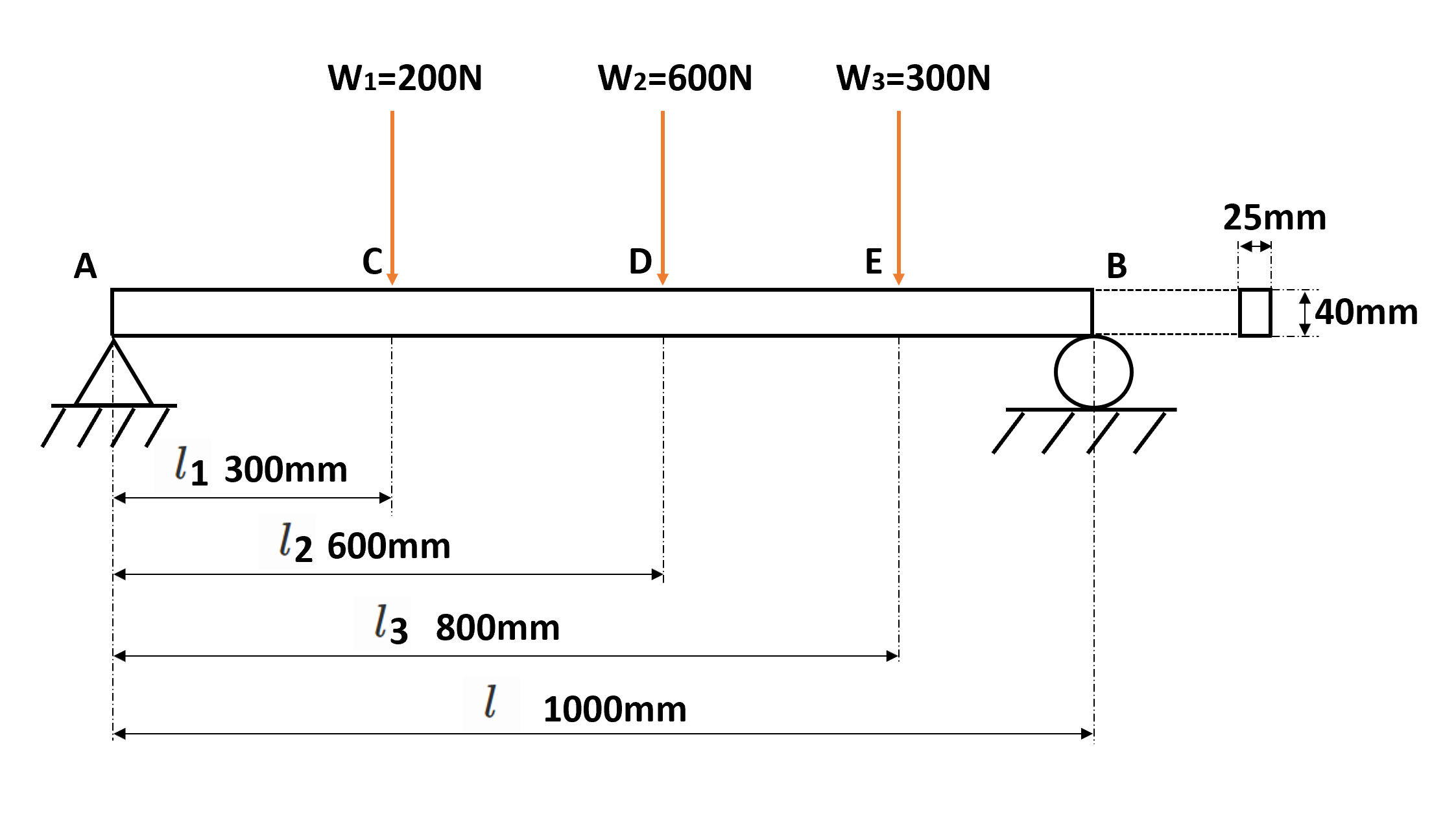
例題の解答
支点反力を求める
すべての外力を足し合わせるとゼロになるという条件から式を立てていきます。
$$W_{1}+W_{2}+W_{3}-R_{A}-R_{B}=0$$
$$R_{A}+R_{B}=W_{1}+W_{2}+W_{3} ・・・(1)外力のつり合い$$
反時計回りのモーメントを+とすると、つりあいの式は、
$$-(W_{1}l_{1}+W_{2}l_{2}+W_{3}l_{3})+R_{B}l=0 ・・・(2)モーメントのつり合い$$
となります。
式(2)より、支点反力RBは、
$$R_{B}=\frac{W_{1}l_{1}+W_{2}l_{2}+W_{3}l_{3}}{l} ・・・(3)支点反力R_{B}$$
となるので、この式(3)へそれぞれ数値をあてはめると、
$$R_{B}=\frac{W_{1}l_{1}+W_{2}l_{2}+W_{3}l_{3}}{l}$$
$$=\frac{200×300+600×600+300×800}{1000}$$
$$=660N$$
一方、RAは式(1)より、
$$R_{A}+R_{B}=W_{1}+W_{2}+W_{3}$$
$$R_{A}+660=200+600+300$$
$$R_{A}=200+600+300-660$$
$$=440N$$
せん断力を求める
$F_{AC}について$
$$F_{AC}=R_{A}=440N$$
$F_{CD}について$
$$F_{CD}=R_{AC}-200$$
$$=440-200$$
$$=240N$$
$F_{DE}について$
$$F_{DE}=F_{CD}-600$$
$$=240-600$$
$$=-360N$$
$F_{EB}について$
$$F_{EB}=F_{DE}-300$$
$$=-360-300$$
$$=-660N$$
曲げモーメントを求める
モーメントの公式、
$$M=FL$$
を使い、それぞれの曲げモーメントを求めます。
$M_{C}について$
$$M_{C}=440×200=88000$$
$$=8.80×10^4Nmm$$
$M_{D}について$
$$M_{C}=440×600=264000$$
$$=26.40×10^4Nmm$$
$M_{E}について(支点Bから計算)$
$$M_{E}=660×200=132000$$
$$=13.20×10^4Nmm$$
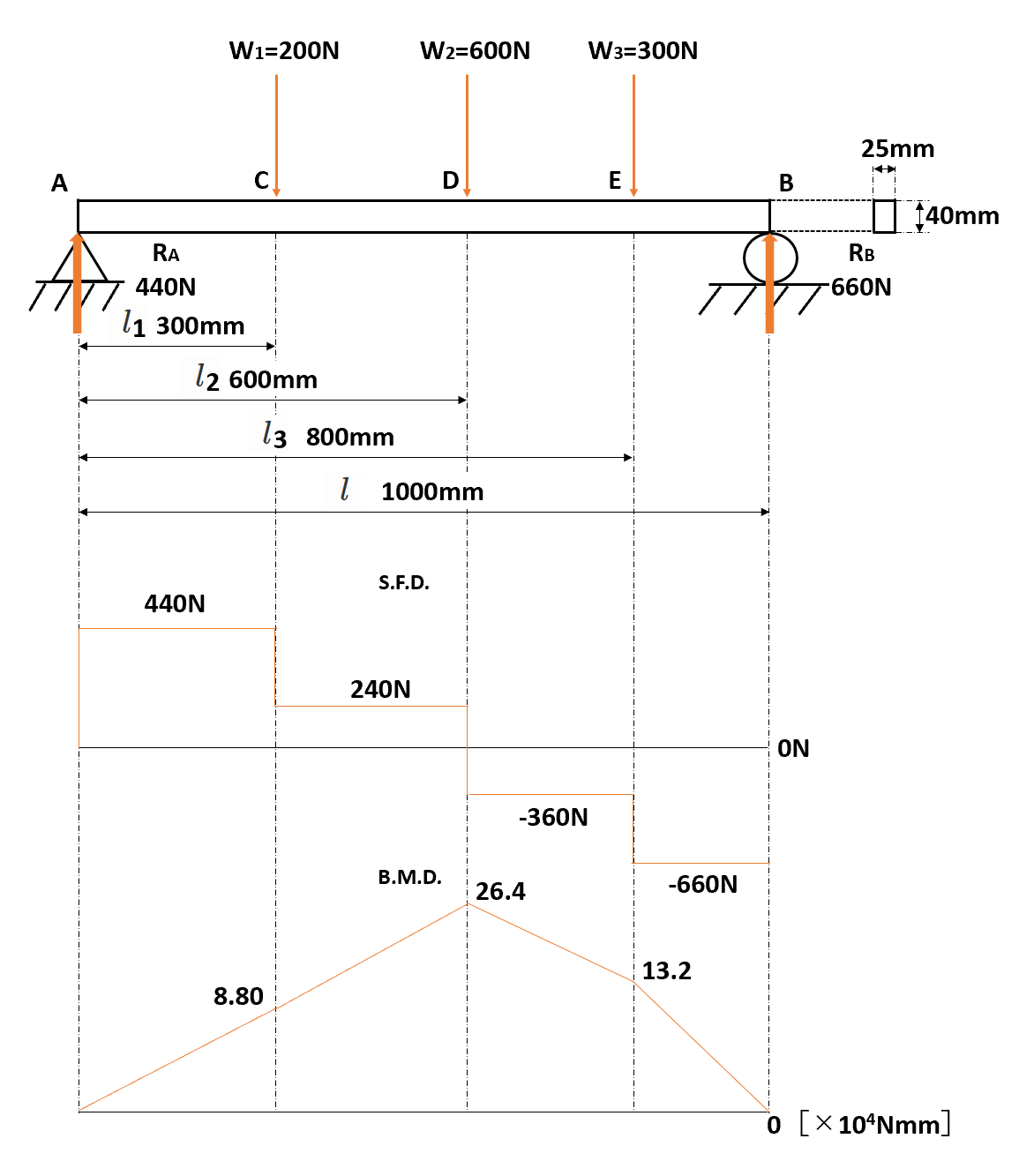
MDを最大曲げモーメントM、断面係数をZと置き、曲げ応力σを求める
最後に、曲げ応力σの公式、
$$σ=\frac{M}{Z}$$
を使い、求めていきます。
ここで、今回の材料では断面係数Zは、
$$Z=\frac{1}{6}bh^2$$
を使い計算します。
$$σ=\frac{M}{Z}$$
$$=\frac{\frac{26.40×10^4}{1}}{\frac{bh^2}{6}}$$
$$=\frac{6×26.40×10^4}{bh^2}$$
ここで、h=40mm、b=25mmをそれぞれ上式に代入すると、
$$=\frac{6×26.40×10^4}{bh^2}$$
$$=\frac{6×26.40×10^4}{25×40^2}$$
$$=39.60MPa$$
はりの縦と横を置き換えた場合
同じ荷重条件下で、今度ははりを横長断面で使用した場合の曲げ応力σを求めていきます。
今回の問題では荷重の条件が変わらないことから、最大曲げモーメントも変わりません。よってbとhの数値だけを変えれば計算できます。
$$σ=\frac{M}{Z}$$
$$=\frac{\frac{26.40×10^4}{1}}{\frac{bh^2}{6}}$$
$$=\frac{6×26.40×10^4}{bh^2}$$
$$=\frac{6×26.40×10^4}{40×25^2}$$
$$=63.36MPa$$
解:曲げ応力σは39.60MPa、横長断面で使用した場合の曲げ応力σは63.36MPa
まとめ
本記事では、両端支持はりに集中荷重は作用している場合を想定し、支点反力の計算からせん断力図 (S.F.D)、曲げモーメント図 (B.M.D) を作成し、そこから実際に曲げ応力を求める一連の流れを解説しました。
今回ご紹介した内容と計算方法を学ぶことで、断面形状をどのように選定すれば強度と軽量化のバランスをうまく両立できるか、そのポイントと落としどころもつかめるようになります。
ぜひ、材料力学以外の分野(各種部材の選定や構造解析を行う際)でも参考にしてみてください。
