はりに発生する曲げ応力の許容値を設定し、最大曲げモーメントと断面係数からはりの断面寸法を求めていきたいと思います。
材料力学が初めての方でも構えずに読んでいただけるよう、なるべく噛みくだいた言い方でまとめてみましたので、気軽にチェックしてみてくださいね。
はじめに:断面係数と曲げ応力の基礎知識
今回、はりの断面寸法を求める際に大切となるのが、断面係数Z(section modulus)と曲げ応力σ(bending stress)です。
断面係数Z(section modulus)とは
断面係数Zは、断面二次モーメント Iを中立軸から断面上端までの距離yで割った値のことをいいます。
断面係数は、材料の断面形状によってそれぞれ異なる計算式があります。例えば、矩形断面(長方形断面)の場合、幅をb、高さをhとすると、
$$Z=\frac{1}{6}bh^2$$
という式になります。
ここの断面係数Zについての内容、断面係数Zの公式一覧について知りたい方は下の記事にて取り扱っていますので、併せてご覧ください。

曲げ応力σ(bending stress)
曲げ応力σは、曲げモーメントMを受けた際、部材内部で変形しようと発生する応力のことをいいます。
部材の中心軸付近を境に、上側が圧縮力、下側が引張力を受ける状態となり、このときの断面内で発生している応力分布のことを「曲げ応力」と呼びます。
曲げ応力を求める公式は、次式で表されます。
$$σ=\frac{M}{Z}$$
σ:曲げ応力(MPa)
M:最大曲げモーメント(Nmm)
Z:断面係数(mm3)
この式より、同じ強さの曲げモーメントを受けても、断面係数Zが大きければ曲げ応力は小さくなります。つまり、同じ荷重条件であれば、より大きな断面係数をもつ断面形状のほうが曲げ応力を低く抑えられ、強度的に有利になってくるというわけです。
ここの曲げ応力σについて知りたい方は下の記事にて取り扱っています。

曲げ応力と許容応力の関係について
材料力学では、曲げ応力が材料の許容応力(あるいは設計上設定した許容値)を超えないように、断面形状や寸法を決定します。たとえば、許容応力σaを60MPaと設定した場合、
$$σ=\frac{M}{Z}≤σ_{a}$$
となるように断面を計算する必要があるわけです。
このように計算しなければいけない理由は、材料(もしくは製品)に安全性や耐久性を確保するためです。材料にはそれぞれ「これ以上の応力がかかると破損や永久変形が起こる」という限界点があり、そこを超えると構造物として機能を失う可能性が高まります。
このことから、材力や設計における“許容応力”というのは、ここまでの応力だったら部材にかかってもいいよという応力の上限値を示しているということになります。
許容できる応力=許容応力と覚えておけばわかりやすいですね。
以上の内容を踏まえて、次は以下のような例題に取り組んでいきたいと思います。
計算問題
例題1
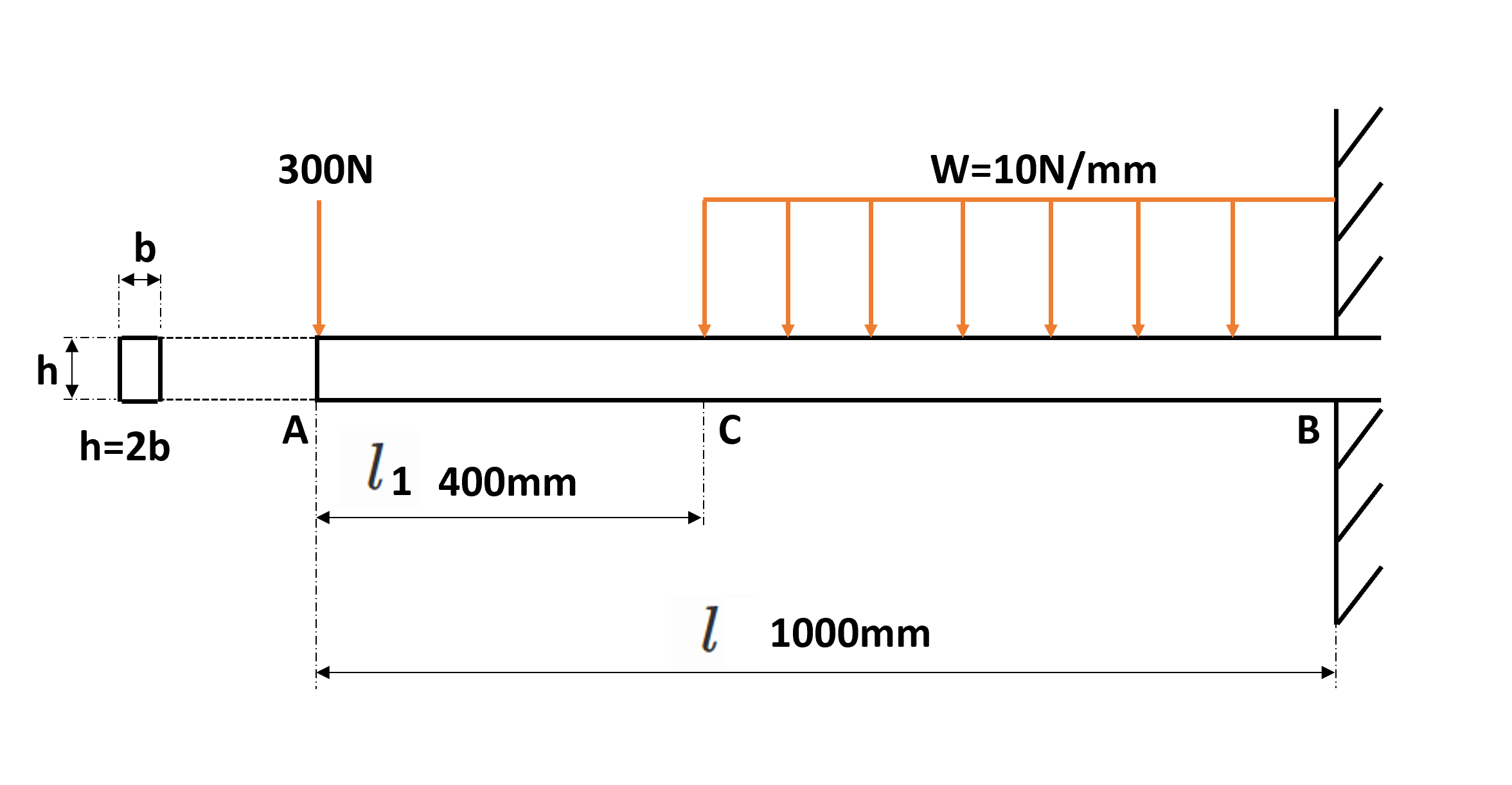
以下のような集中荷重と等分布荷重を受ける片持ちはりの許容応力を60MPaとしたとき、幅の2倍の高さを持つ長方形断面の寸法を計算しなさい。
例題1の解答
支点反力の計算
$$R_{B}=300+10×600$$
$$=6300N$$
せん断力の計算
AC間について
片持ちはりに集中荷重1つかかっているときのせん断力は、集中荷重wに相当するので、
$$F_{AC}=-300N$$
CB間について
集中荷重300Nに自由端からの距離をxとして、等分布荷重を加える。
$400≦x≦1000の一般式$
$$F_{CB}=F_{AC}-w(x-400)$$
$$=-300-10(x-400)$$
$$=-300-10x+4000$$
$$=-10x+3700$$
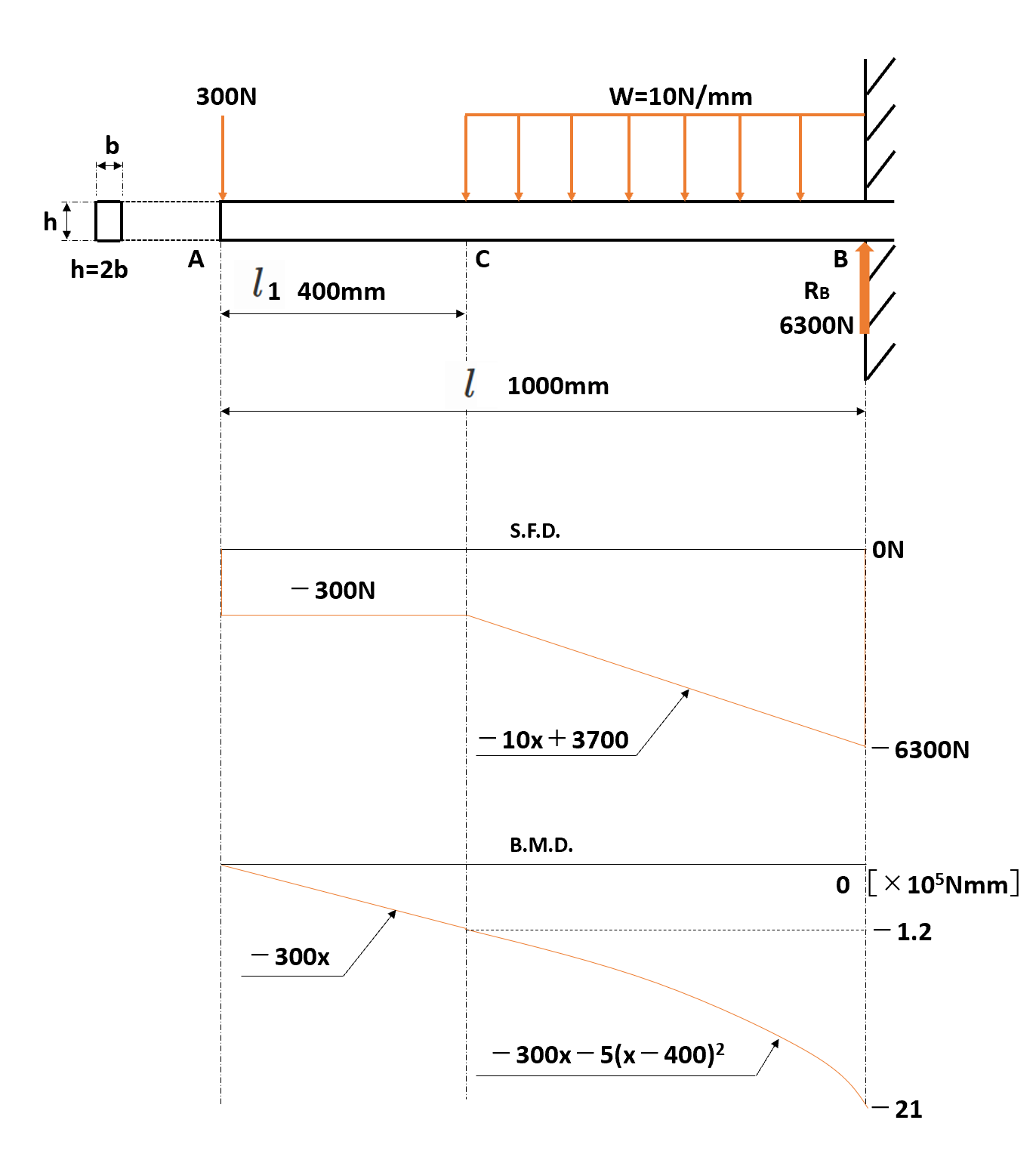
曲げモーメントの計算
AC間について
任意の断面から集中荷重までの距離をxとすると、
$$M_{AC}=-300x$$
となります。点Cのモーメントについては、上式へx=400mmを代入すると、
$$M_{C}=-300x$$
$$=-300×400$$
$$=-1.20×10^5Nmm$$
と求めることができます。
CB間について($400≦x≦1000$)
任意の断面から自由端までの距離x間の全モーメントを加える式を立てます。
$$M_{CB}=-300x-\frac{W}{2}(x-400)^2$$
$$=-300x-\frac{10}{2}(x-400)^2$$
$$=-300x-5(x-400)^2$$
固定端Bについて
固定端Bに発生する最大曲げモーメントを求める際は、上式を引用して求めていきます。
$$=-300x-\frac{W}{2}(x-400)^2$$
$$=-300×1000-\frac{10}{2}(1000-400)^2$$
$$=-2100000Nmm$$
$$=-21.00×10^5Nmm$$
曲げ応力σから幅bを求める
曲げ応力の公式は、
$$σ=\frac{M}{Z}$$
です。ここ式へ$Z=\frac{1}{6}bh^2$を代入していくのですが、hは2bに相当するということだったので、
$$Z=\frac{1}{6}bh^2$$
$$=\frac{1}{6}b(2b)^2$$
$$=\frac{1}{6}b(2b)^2$$
$$=\frac{1}{6}b×4b^2$$
$$=\frac{4b^3}{6}$$
となり、これを曲げ応力σの式へ代入します。
一方で、Mは先ほど求めた固定端Bに発生している最大曲げモーメントMを、この式に代入します。すると、
$$σ=\frac{M}{Z}$$
$$=\frac{M}{\frac{4b^3}{6}}$$
$$=\frac{6M}{4b^3}$$
となります。ここで、この式を幅bについての式へ変換します。
$$σ=\frac{6M}{4b^3}$$
$$σ×\frac{4}{6M}=\frac{\cancel{6}\cancel{M}}{\cancel{4}b^3}×\frac{\cancel{4}}{\cancel{6}\cancel{M}}$$
$$\frac{4σ}{6M}=\frac{1}{b^3}$$
$$b^3=\frac{6M}{4σ}$$
$$b=\sqrt[3]{\frac{6M}{4σ}}$$
幅bについての式が導けたので、この式へそれぞれの数値を代入すると、
$$b=\sqrt[3]{\frac{6M}{4σ}}$$
$$=\sqrt[3]{\frac{6×21.00×10^5}{4×60}}$$
$$=37.44436・・・$$
$$b=37.44mm$$
となります。
h=2bという関係から、断面寸法を求める
幅bが37.44mmと判明したので、高さhは、
$$h=2b$$
$$=2×37.44$$
$$=74.88mm$$
となります。
解:断面寸法はb=37.44mm、h=74.88mm
例題2
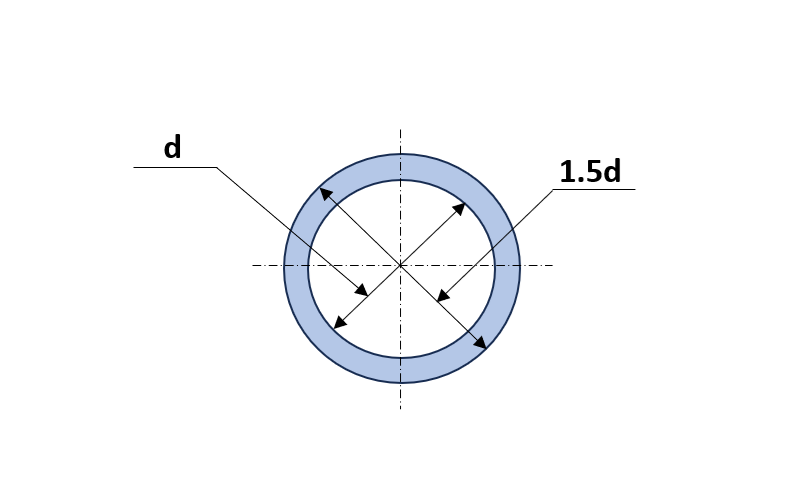
例題1と同じ条件で、今度ははりを中空パイプに交換します。このときパイプの内径をd、外径を1.5dとしたときのパイプの内径を計算しなさい。
例題2の解答
断面係数Zの計算
例題1より求めた断面寸法から、断面係数Zは、
$$Z=\frac{1}{6}bh^2$$
$$=\frac{37.44×74.88^2}{6}$$
$$=34987.7698・・・$$
$$=34987.77mm^3$$
内径dの計算
内径d、外径1.5dのときの中空パイプの断面係数Zは、
$$Z=\frac{π×(1.5d)^4-d^4}{32×1.5d}$$
$$=\frac{π×5.0625d^4-d^4}{32×1.5d}$$
$$=\frac{π×4.0625d^4}{32×1.5d}$$
$$=0.26589000・・・d^3$$
$$=0.27d^3$$
となります。Zは先ほど求めているので、この式に当てはめると、
$$34987.77=0.27d^3$$
$$d^3=\frac{34987.77}{0.27}$$
$$d=\sqrt[3]\frac{34987.77}{0.27}$$
$$=50.60mm$$
解:内径50.60mm
まとめ
今回は、最大曲げモーメントと断面係数からはりの断面寸法を求めていきました。
どんな材料や荷重条件が与えられても、「許容応力を超えない設計」を意識することで安全な構造が実現できます。
はりの断面寸法を求めるうえで必要となる曲げ応力や断面係数の考え方を、少しでも理解いただけたなら幸いです。
