支点反力を計算する方法に悩んでいませんか?
この記事では力学初心者にもわかりやすいように、両端支持はりを用いて支点反力の計算手順を丁寧に解説します。
これを読めば、支点反力の基本的な計算が自信を持ってできるようになります。
それでは一緒に学んで力学を得意科目にしましょう!
両端支持はり(単純支持梁)とは?
両端支持はり(りょうたんしじはり)は、材料力学でよく出てくる構造の一種で、はりの両端が支えられている状態のことを指します。この支え方には以下のような特徴があります。
支点の形状
両端支持はりでは、片方の端が「回転と移動ができる移動支点(ローラー支点)」で、もう片方が「回転のみできる回転支点(ピン支点)」で支えられています。
これにより、はりは水平方向の動きを制限されながらも、回転は自由にできる状態となっています。
ポイント:支持形式の種類
支点の支持は、以下の3種類の方法があります。
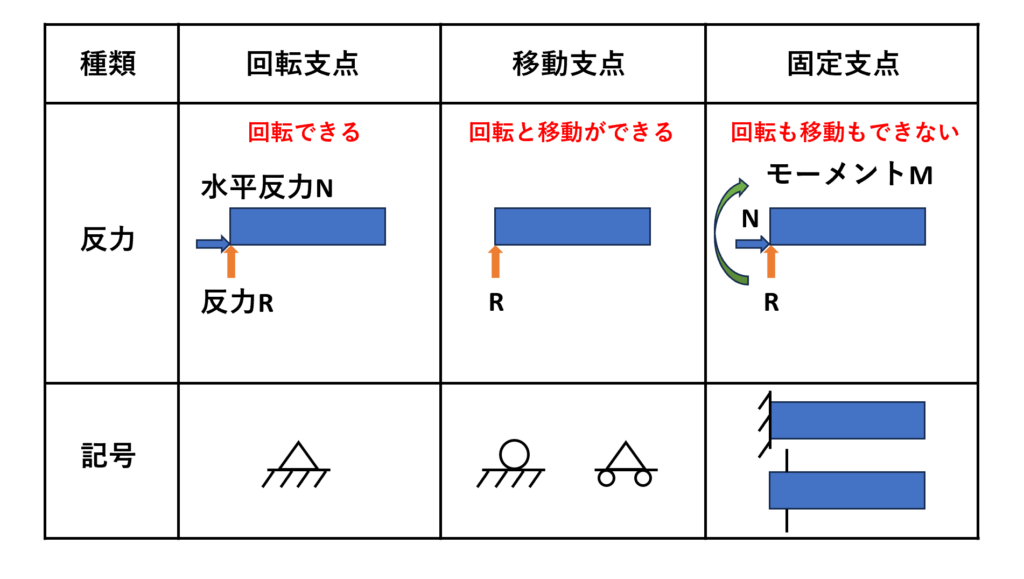
荷重の受け方
両端支持はりは、はりの上にかかる外力(荷重)を2つの支点で受け止めます。
このとき、両支点に「支点反力」という荷重とは逆向きの力が発生し、はりは平衡を保ちます。
例えば、一本の板の両端をレンガで支えたとしましょう。その上に人が立った場合、人の重み(荷重)は板にかかり、その力が両端のレンガ(支点)に伝わります。
このときレンガが支点反力を提供し板を支えるという構造が、両端支持はりの働きです。
両端支持はり以外の支持形式
両端支持はり以外の支持形式では、
①片持ち梁
②両端固定梁
があります。
詳しくは、以下の記事をご確認ください。

支点反力の計算
今回は両端支持はりに、3つの集中荷重が作用している場合で考えていきます。
下向きの力を+、反時計回りのモーメントを+として、支点Aを基準にします。
計算方法は、力の総和と力のモーメントの総和がゼロという条件を使って求めていきます。
具体的にはまず支点Bの反力RBを求め、次に支点Aの反力RAを求めるという内容で計算を進めていきます。
順番に見ていきましょう。
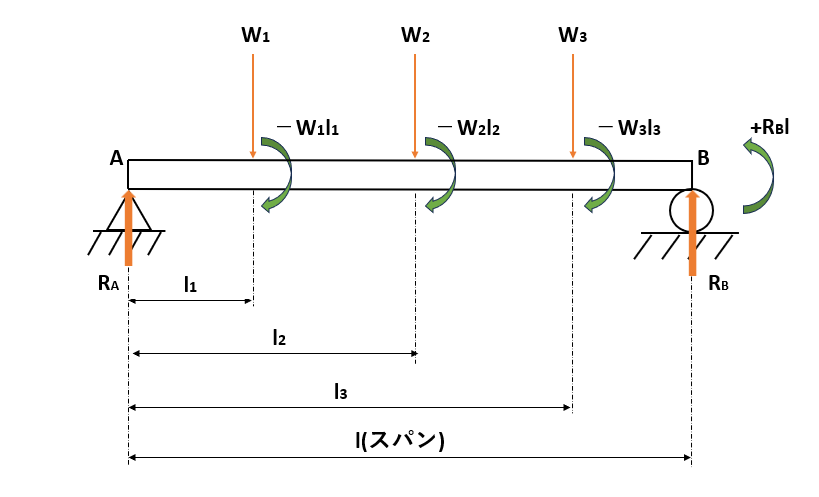
最初にすべての外力を足し合わせるとゼロになるという式を立てていきます。
外力は荷重W1、W2、W3と支点反力RA、RBの5つあるので、
$$W_{1}+W_{2}+W_{3}-R_{A}-R_{B}=0$$
$$R_{A}+R_{B}=W_{1}+W_{2}+W_{3} ・・・(1)外力のつり合い$$
と書き表せます。
次にモーメントのつり合いを立式します。
反時計回りのモーメントを+としたので、つりあいの式は、
$$-(W_{1}l_{1}+W_{2}l_{2}+W_{3}l_{3})+R_{B}l=0 ・・・(2)モーメントのつり合い$$
となります。
ステップ2で立てた式を使って、支点反力RBを求める形に式変形します。式(2)より、
$$R_{B}=\frac{W_{1}l_{1}+W_{2}l_{2}+W_{3}l_{3}}{l} ・・・(3)支点反力R_{B}$$
となります。
算出した支点反力RBを式(1)に代入して、反力RAを求めます。式(1)より、
$$R_{A}=W_{1}+W_{2}+W_{3}-R_{B} ・・・(4)支点反力R_{A}$$
が得られます。
以上の流れで支点反力RA、RBが求まります。
次は実際に問題を解いていきましょう。
計算問題
例題1
次のような両端支持はりに荷重1000Nが作用した時の支点反力を求めなさい。力のベクトルの長さは概略とします。

例題1の解答
力のモーメントの総和がゼロなので、
$$R_{B}=\frac{Wl_{1}}{l}=\frac{1000×300}{800}$$
$$=375N$$
力の総和がゼロなので、
$$R_{A}=W-R_{B}$$
$$R_{A}=1000-375=625N$$
解:RA=625N、RB=375N
例題2
次のような両端支持はりで複数の集中荷重が作用した場合の支点反力を求めなさい。力のベクトルの長さは概略とします。

例題2の解答
力のモーメントの総和がゼロなので、
$$R_{B}=\frac{W_{1}l_{1}+W_{2}l_{2}+W_{3}l_{3}}{l}$$
$$=\frac{300×250+1000×500+700×750}{1000}$$
$$=1100N=1.1kN$$
力の総和がゼロなので、
$$R_{A}=W_{1}+W_{2}+W_{3}-R_{B}$$
$$=300+1000+700-1100$$
$$=900N$$
解:RA=900N、RB=1100N(1.1kN)
まとめ
今回は両端支持はりの計算方法について解説しました。
求め方や公式について理解していただけたかと思います。
この記事では支点反力の求め方にフォーカスした内容にしたかったため、はりに加わる曲げモーメントの大きさを示したBMD(Bending Moment Diagram)という図やはりに加わるせん断力の大きさを示したSFD(Shear Force Diagram)という図につきましては、また別記事にて紹介したいと思います。
両端支持はりは構造力学や実務で頻繁に用いられるので、これらの計算方法はぜひ覚えておきましょう。
