材料科学や工学の分野で頻繁に登場する「縦弾性係数」という言葉。実はこの縦弾性係数は、私たちの身近な物質がどのように変形するかを理解する上で非常に重要な役割を果たしています。
例えば、建築物の強度や機械部品の耐久性を評価する際にもこの縦弾性係数というのはよく出てきます。この言葉の意味と特性について、皆さんはどれぐらいご存知でしょうか?
この記事では縦弾性係数とは何か、その基本的な概念を応力-ひずみ線図を絡めて解説していきたいと思います。
応力とひずみ
まず最初に応力とひずみについて解説します。
応力とひずみは、物体が外力を受けたときの変形や内部の力の状態を理解するための基本的な概念です。
応力(Stress)とは?
応力は、物体が外力を受けたときに内部で発生する「単位面積あたりの力」を意味します。
単位はPa(パスカル)で、1 Pa は 1 N/m² です。材料力学では、応力の単位がめちゃめちゃでかくなってしまうので、MPa(メガパスカル)に置き換えてすっきり計算していきます。
応力の式は、以下のようにあらわします。
$$σ=\frac{P}{A}$$
σ:応力(N/mm)
P:外力(N)
A:断面積(mm2)
この公式はとっても重要ですので、ぜひ覚えてください。
ひずみ(Strain)とは?
ひずみとは、物体が応力によってどれだけ変形したかを表す「変形の割合」のことをいいます。
例えば、物体に引っ張る力を加えた場合、その力の方向に伸びる変形が発生します。このときの伸びた量が変形量であり、その変形量を元の長さで割った値がひずみとなります。
ひずみの単位は無次元(単位なし)です。
ひずみの公式
材料力学でよく出てくるひずみは主に以下の3種類です。
縦ひずみ
縦ひずみは、ギリシャ文字のε(イプシロン)で表されます。
$$ε=\frac{λ}{l}$$
横ひずみ
横ひずみ は、ギリシャ文字のε’(イプシロンダッシュ)で表されます。
$$ε’=\frac{δ}{d}$$
せん断ひずみ
せん断ひずみは、ギリシャ文字のγ(ガンマ)で表されます。
$$γ=\frac{λ}{l}$$
そして、このひずみというのはポアソン比を扱う際にもよく出てきます。以下の記事に詳しく記載していますので、興味があればご覧いただければと思います。

応力-ひずみ線図
次に応力-ひずみ線図についてです。
応力-ひずみ線図は材料の力学的性質を示すグラフの一つで、材料が力を受けたときの「応力」と「ひずみ」の関係を表したものです。
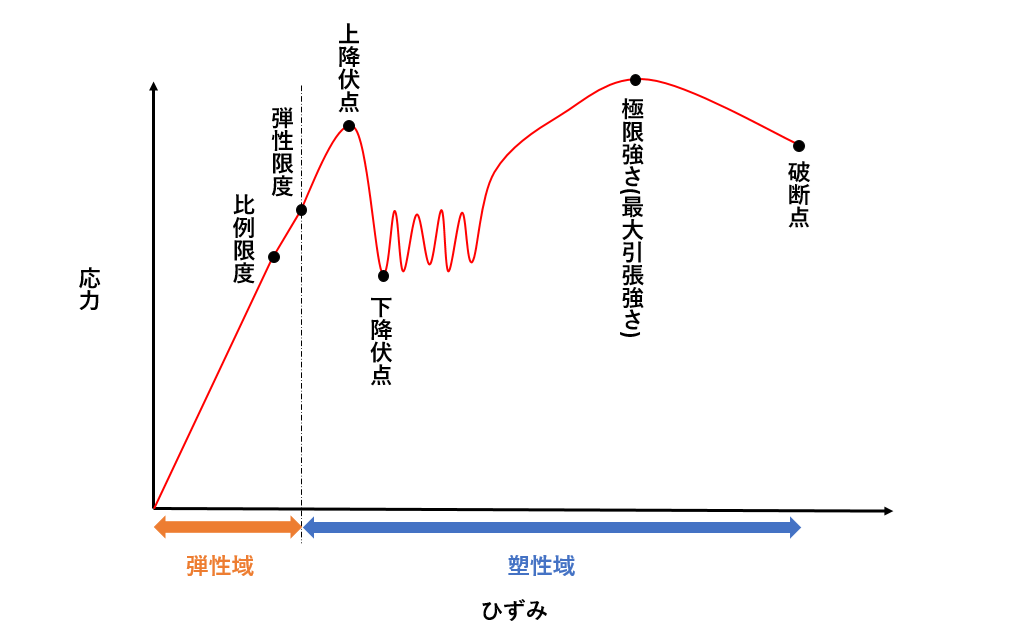
この線図は、材料の強度や変形の特性を把握するために使われます。
鉄や鋼では上図のような曲線を描くため明確な降伏点が見られることが多いですが、ガラスやセラミックスなどの脆性材料では降伏点がはっきりせず、破断まで直線的な挙動を示します。
また、アルミニウムや銅などの延性の高い材料においては、降伏後に大きな塑性変形を示し、ガラスやセラミックスなどの脆性材料では、塑性変形をほとんど示さずある点を境に急に破断します。
縦弾性係数とは?
応力-ひずみ線図では、応力とひずみが比例する領域(表でいうと直線になっているところ)があります。
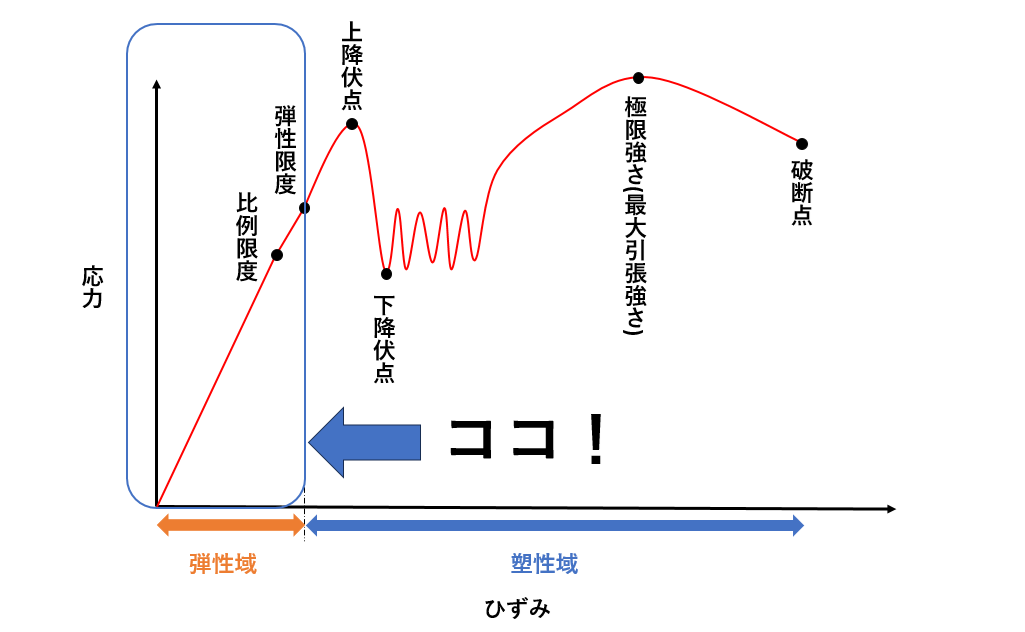
この比例している範囲は弾性範囲と呼ばれ、この範囲までは力を取り除けば元の形状に戻る弾性という性質を持っています。
縦弾性係数というのは、ここの比例している直線の応力σを縦ひずみε(イプシロン)で割った弾性定数のことです。
そしてこの弾性定数は縦弾性係数E、またはヤング率ともいいます。
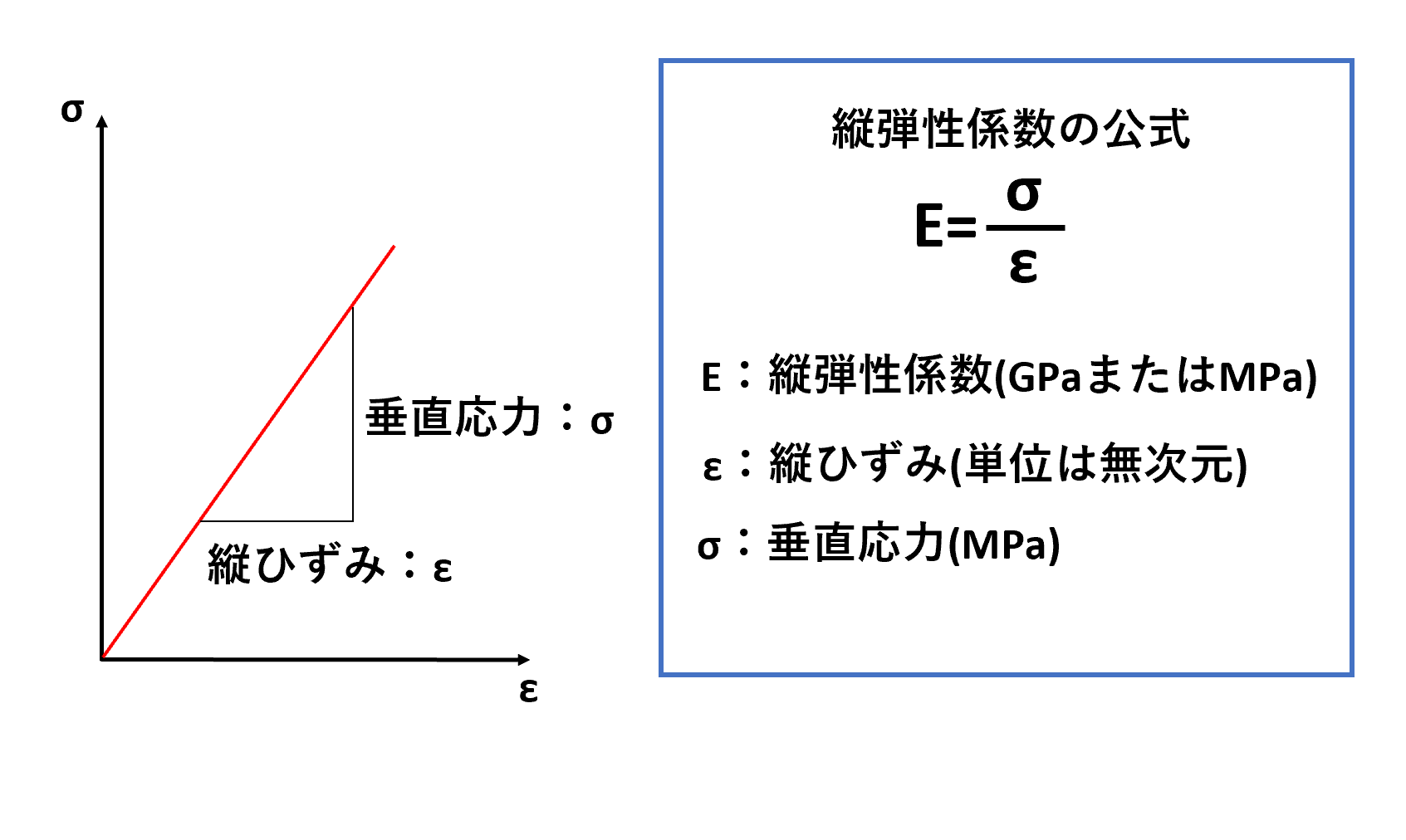
縦弾性係数の単位は応力を無次元のひずみで割って計算しますが、MPaだと計算結果の値が大きくなってしまいます。
そのため縦弾性係数Eは一般的にGPaのほうがよく使われています。
フックの法則
物体が外力(荷重)を受けて弾性変形を起こすとき、外力が大きくなるにつれて物体の変形も大きくなります。
多くの材料は、外力が特定の限界値を超えない範囲では、外力と変形量の間に単純な比例関係が成り立ちます。
この関係を「フックの法則」と呼びます。
また、この比例関係にある範囲のことを弾性域と呼び、変形後元の形状に戻らなくなる領域のことを塑性域と呼びます。
フックの法則を応力-ひずみ線図にあてはめて考える場合、次式のような関係が成立します。
$$σ = Eε$$
σ :垂直応力
E:縦弾性係数
ε:縦ひずみ
縦弾性係数Eの求め方
縦弾性係数Eを求めるときの垂直応力σは元の材料の断面積Aと荷重Pで決まります。
そして、ひずみεについては材料の元の長さl(エル)と変形量λ(ラムダ)で決まります。
そしてこれらの条件を用いると、縦弾性係数Eというのは次のように表すことができます。
$$縦弾性係数E=\frac{σ}{ε} ・・・(1)$$
$$垂直応力σ=\frac{P}{A} ・・・(2)$$
$$縦ひずみε=\frac{λ}{l} ・・・(3)$$
縦弾性係数Eの式に②と③を代入すると
$$E=\frac{σ}{ε}=\frac{\frac{P}{A}}{\frac{λ}{l}}=\frac{Pl}{Aλ}$$
$$縦弾性係数E=\frac{Pl}{Aλ} ・・・(4)$$
次の項目では、縦弾性係数を扱った問題を掲載しています。
計算問題
例題1
40MPaの引張応力が発生していて、材料のひずみが0.00028の時、この材料の縦弾性係数を求めなさい。
ポイント
この問題は縦弾性係数E(ヤング率)の公式を使って計算できます。
例題1の解答
先ほどの縦弾性係数の公式を使い、それぞれ数値を代入。
$$E=\frac{σ}{ε}=\frac{40}{0.00028}=\frac{40}{28×10^{-5}}$$
$$=142,857.714MPa$$
解:E=142.86GPa
例題2
長さ1m、直径30mm、縦弾性係数206GPaの丸棒に30kNの引張荷重を与えた。この時の縦ひずみと変形量を求めなさい。
ポイント
荷重と変形量の関係で解説した3つの式を思い出すと簡単に計算できます。
例題2の解答
①変形量ラムダの導出
縦弾性係数Eの公式
$$E=\frac{Pl}{Aλ}$$
から変形量λを求めます。式変形すると以下のような形になります。
$$E=\frac{Pl}{Aλ}$$
$$\frac{A}{Pl}×E=\frac{Pl}{Aλ}×\frac{A}{Pl}$$
$$\frac{AE}{Pl}=\frac{1}{λ}$$
$$λ=\frac{Pl}{AE}$$
この材料は丸棒なので、断面積Aは
$$A=\frac{πD^2}{4}$$
この式をAの部分に当てはめていきます。
$$λ=\frac{Pl}{AE}=\frac{\frac{Pl}{1}}{\frac{πD^2E}{4}}=\frac{4Pl}{πD^2E}$$
この式にそれぞれ数値を入れてλを求めます。
$$λ=\frac{4Pl}{πD^2E}$$
$$=\frac{4×30×10^3×1×10^3}{π×30^2×206×10^3}$$
$$=0.21mm$$
②縦ひずみの導出
先ほど求めたλの数値0.21mmと縦ひずみの式
$$ε=\frac{λ}{l}$$
を使ってεを求めます。
$$ε=\frac{λ}{l}=\frac{0.21}{1×10^3}=0.000210$$
$$=2.10×10^{-4}$$
解:変形量λ0.21mm、ひずみ2.10×10-4または0.02%
まとめ
縦弾性係数は、材料の力学的特性を理解する上で非常に重要な指標です。
特に構造物の設計や材料選定においては、縦弾性係数を考慮することが安全性や性能を確保するために不可欠な要素となります。
今回の計算問題を通じて実際に数値を扱うことで、この概念がより具体的に理解できたことと思います。
今後もこの知識を基に、さらに深い理解を深めていきましょう。
