圧縮荷重を受ける２つの丸棒材料の計算問題

2024年9月9日2025年2月24日

圧縮荷重は、さまざまな構造物や材料において避けて通れない力の一つです。

本記事では二つの材料がこの圧縮荷重にさらされた場合、どのように影響するのかを計算で調べていきます。

それぞれの材料に加わる力学的特性や挙動を理解し、実際の問題例を交えながらその背後にある原理を明らかにしていきます。

圧縮荷重とは？
圧縮荷重以外の荷重はどんなものがある？
計算問題
1. 例題
2. 例題の解答
圧縮荷重の面白い話

圧縮荷重とは？

圧縮荷重とは、物体に対して押しつける力のことを指します。別名、外力とも言います。

シンプルに外から加わる「力」と考えてOKです。

この力が物体を縮めようとする作用を持ち、主に建築や機械工学などの分野で重要な役割を果たします。

身近な例としては、椅子に座ると自分の体重が椅子の脚に圧縮荷重としてかかります。椅子の脚はその体重に耐えられるように支えているので、この状態が圧縮荷重ということになります。

圧縮荷重は物体の設計や材料選定において非常に重要な要素であり、適切に考慮されないと構造物が破損する原因とななったりすることもあるため、重要な要素となります。

圧縮荷重以外の荷重はどんなものがある？

構造物や機械設計で扱う荷重には、圧縮荷重以外にもさまざまな種類があります。

引張荷重（Tensile Load）
概要:：部材を引っ張る力。
身近な例：ワイヤーやロープが荷物を吊るす場合。
影響:：材料が伸びる方向に変形し、破断強度を超えると材料はちぎれる。

せん断荷重（Shear Load）
概要: 部材の断面をスライドさせるような力。
身近な例: ハサミの刃が物を切るとき、リベットやボルトにかかる横方向の力がこれにあたります。
影響: 部材がずれることで破断や変形が発生する。

曲げ荷重（Bending Load）
概要：部材を曲げる方向に働く力。
身近な例：梁（はり）にかかる重さや風の力など。
影響:：部材内部で圧縮応力と引張応力が同時に発生することから、曲げ剛性が重要となる。

衝撃荷重（Impact Load）
概要：短時間に急激に加わる大きな力。
身近な例：ハンマーで打撃を与える場合。
影響：大きな応力が瞬時に発生するので、破壊や変形を引き起こす。

繰り返し荷重（Cyclic Load）
概要：同じ箇所に何度も繰り返しかかる荷重。
身近な例：飛行機の翼が風に揺られる際の荷重。
影響：同じ個所に継続的に荷重がかかるため、金属疲労や亀裂が発生しやすい。

ほかにも、時間とともに変化する動的荷重（Dynamic Load）や、部材の中心線から外れた位置にかかる偏心荷重（Eccentric Load）などがありますが、材料力学でよく出てくる荷重は上記５つと本記事の圧縮荷重の計6つになります。

計算問題

例題

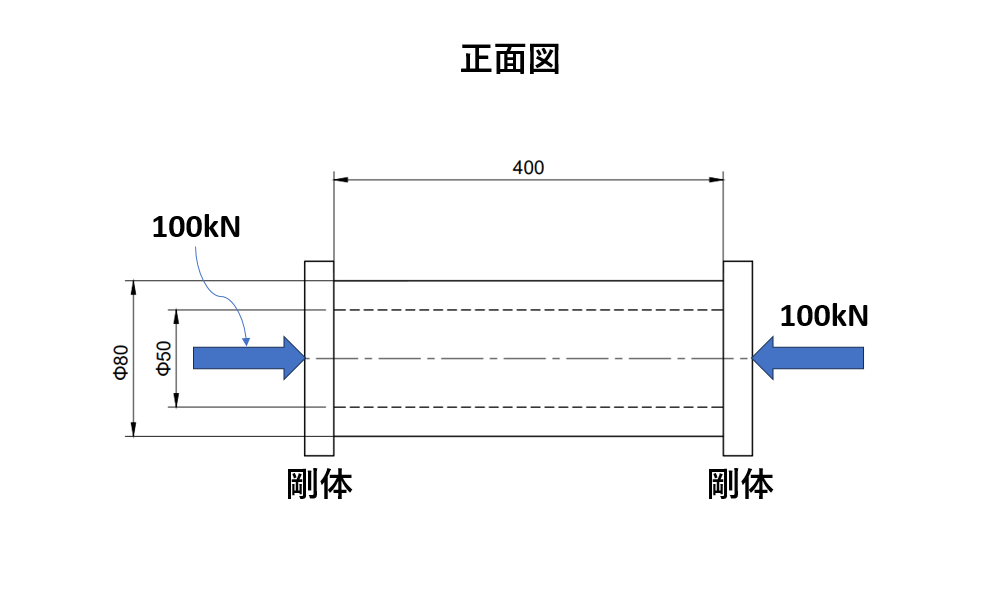
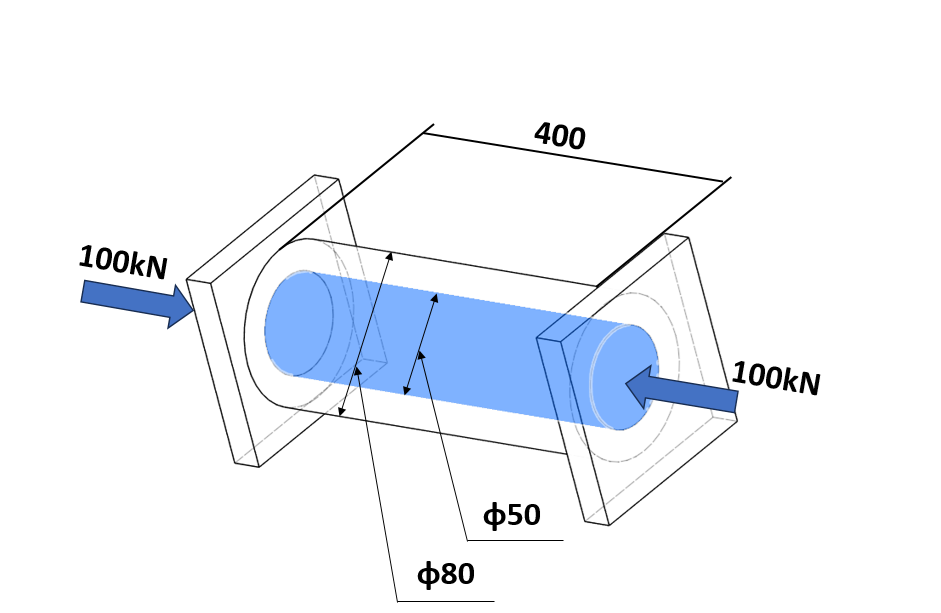
外径80mm、内径50mmの中空パイプAと直径50mmの丸棒Bを組み合わせた長さ400mmの部材がある。この両端に変形を無視できる剛体があり、その剛体を介して100kNの圧縮荷重が作用している。中空パイプAの縦弾性係数(ヤング率：E)を200GPa、丸棒Bの縦弾性係数(ヤング率：E)を100GPaとしたとき、それぞれの部材に発生する応力と部材全体の圧縮量を計算しなさい。

今回の内容のキーポイント

この問題では、２つの異なる部材が剛体壁を介して圧縮荷重を受けた場合の内容ですが、以下の内容をおさえて計算を進めるとより理解しやすいと思います。

AとBそれぞれの部材に発生している応力は異なる。
AとBのひずみと圧縮量は等しい。
圧縮荷重100kNをP、AとBに作用する荷重をそれぞれP₁、P₂とする。
AとBに発生する応力をσ₁、σ₂、圧縮量をλとする。

STEP

AとBそれぞれの部材に発生している応力は異なる。

応力 (σ)は材料に作用する力を断面積で割ったものです。式で表すと以下のようになります。

$σ = \frac{P}{A}$

中空パイプAと丸棒Bではそれぞれの断面積が異なるため、同じ荷重でもそこで発生している応力は異なります。

STEP

AとBのひずみと圧縮量は等しい。

今回の問題では、部材A（中空パイプ）と部材B（丸棒）の両端に変形を無視できる剛体が存在します。この剛体は部材Aと部材Bの変形を一体的に制御します。２つの剛体で挟まれているため、部材全体の変形が均一になります。したがって以下のような式が成り立ちます。(ちなみにココの導出方法は解答欄に記載しています。)

$\frac{σ_{1}}{E_{1}} = \frac{σ_{2}}{E_{2}}$

STEP

圧縮荷重100kNをP、AとBに作用する荷重をそれぞれP1、P2とする。

今回の問題では、全体にかかる荷重は100kNです。この荷重は、それぞれ部材Aと部材Bに分配されます。なので、このような式が成り立ちます。(ココの導出方法も解答欄に記載しています。)

$P = P_{1} + P_{2} = A_{1} σ_{1} + A_{2} σ_{2}$

STEP

AとBに発生する応力をσ1、σ2と置き、圧縮量をλとする。

今回の剛体に挟まれた２つの部材問題からσ₁、σ₂の式を導出する場合、ステップ②と③で紹介した以下の２つの関係式

$P = P_{1} + P_{2} = A_{1} σ_{1} + A_{2} σ_{2}$

$\frac{σ_{1}}{E_{1}} = \frac{σ_{2}}{E_{2}}$

を使ってそれぞれのσを求める必要があります。

さらに圧縮量λは次式で計算していきます。

$圧縮量 λ ＝ \frac{l}{E_{1}} \times σ_{1} ＝ \frac{l}{E_{2}} \times σ_{2}$

例題の解答

【1】AとBそれぞれに発生する応力σ₁、σ₂を計算する。

圧縮荷重PはP₁とP₂に分散するため、以下の式が成立する。

$P = P_{1} + P_{2} ・・・ (1)$

ここでこのP₁とP₂というのは、応力の式

$σ = \frac{P}{A}$

の式のPというところに相当するので、この式を変形しP=~~~という形に式変形する。式変形したら、先ほどの

$P = P_{1} + P_{2}$

に代入する。

$σ = \frac{P}{A}$

$A \times σ = \frac{P}{A} \times A$

$P = A σ$

式（1）のP=P₁+P₂に代入

$P = P_{1} + P_{2}$

$= A_{1} σ_{1} + A_{2} σ_{2} ・・・ (2)$

圧縮量が等しいからひずみも等しいので、縦弾性係数Eの公式を式変形し、等式を立てる。

$縦弾性係数： E = \frac{σ}{ε}$

$ε = \frac{σ}{E}$

部材AとBの圧縮量とひずみは等しいので

$\frac{σ_{1}}{E_{1}} = \frac{σ_{2}}{E_{2}} ・・・ (3)$

式（2）と式（3）を使い、σ₁とσ₂を求める。式（3）から

$\frac{σ_{1}}{E_{1}} = \frac{σ_{2}}{E_{2}}$

$E_{2} \times \frac{σ_{1}}{E_{1}} = \frac{σ_{2}}{E_{2}} \times E_{2}$

$σ_{2} = σ_{1} \times \frac{E_{2}}{E_{1}} ・・・ (4)$

この式のままではまだ応力σ_１とσ_２を求めることができません。そこで、ここで得た式（4）を使って、式（2）のσ₂に代入して圧縮荷重を求める。

$P = A_{1} σ_{1} + A_{2} σ_{2}$

$＝ A_{1} σ_{1} + A_{2} σ_{1} \frac{E_{2}}{E_{1}}$

$= σ_{1} (A_{1} + \frac{E_{2}}{E_{1}} A_{2})$

$= σ_{1} \frac{A_{1} E_{1} + A_{2} E_{2}}{E_{1}}$

上記で得た式を使って、応力σを求める(まずはσ₁から)。さらに式変形すると

$P = σ_{1} \frac{A_{1} E_{1} + A_{2} E_{2}}{E_{1}}$

$\frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}} \times P = σ_{1} \frac{A_{1} E_{1} + A_{2} E_{2}}{E_{1}} \times \frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}}$

よって

$σ_{1} ＝ \frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}} \times P$

となる。

σ₂も導出する。式（4）のσ₁に先ほど求めた

$\frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}} \times P$

を代入すると

$σ_{2} = σ_{1} \times \frac{E_{2}}{E_{1}}$

$＝ \frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}} P \times \frac{E_{2}}{E_{1}} ＝ \frac{E_{2}}{A_{1} E_{1} + A_{2} E_{2}} P$

となり、それぞれσ₁、σ₂が求まった。

$σ_{1} ＝ \frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}} \times P$

$σ_{2} = \frac{E_{2}}{A_{1} E_{1} + A_{2} E_{2}} P$

【2】圧縮量λを求める。

縦弾性係数の式

$E = \frac{P l}{A λ}$

をλ＝~~~という形に式変形する。

$E = \frac{P l}{A λ}$

$\frac{A}{P l} \times E = \frac{P l}{A λ} \times \frac{A}{P l}$

$\frac{A E}{P l} = \frac{1}{λ}$

$λ ＝ \frac{P l}{A E} ・・・ (5)$

ここで式(5)の

$\frac{P}{A}$

の部分は応力の式

$σ ＝ \frac{P}{A}$

の式とイコールになっているので、ここをσで表すと

$λ ＝ \frac{l}{E} \times σ ・・・ (6)$

と書き表せる。

式(6)にそれぞれのσ₁、σ₂を代入してあげると以下のような関係式になる。

$圧縮量 λ ＝ \frac{l}{E_{1}} \times σ_{1} ＝ \frac{l}{E_{2}} \times σ_{2} ・・・ (7)$

【3】数値を代入して解を求める。

すべての式が出揃ったので、計算しやすいように式を整え、それぞれの式に数値を代入してあげます。

・応力σ₁(問題文よりd₁=80mm、d₂=50mmとする)

$σ_{1} ＝ \frac{E_{1}}{A_{1} E_{1} + A_{2} E_{2}} P$

$＝ \frac{E_{1}}{\frac{π (d_{1}^{2} - d_{2}^{2})}{4} E_{1} + \frac{π d_{2}^{2}}{4} E_{2}} P$

$= \frac{E_{1} P}{\frac{π (d_{1}^{2} - d_{2}^{2}) E_{1}}{4} + \frac{π d_{2}^{2} E_{2}}{4}}$

$= \frac{\frac{E_{1} P}{1}}{\frac{π (d_{1}^{2} - d_{2}^{2}) E_{1} + π d_{2}^{2} E_{2}}{4}}$

$= \frac{4 E_{1} P}{π (d_{1}^{2} - d_{2}^{2}) E_{1} + π d_{2}^{2} E_{2}}$

$= \frac{4 E_{1} P}{π ((d_{1}^{2} - d_{2}^{2}) E_{1} + d_{2}^{2} E_{2})}$

$＝ \frac{4 \times 200 \times 10^{3} \times 100 \times 10^{3}}{π ((80^{2} - 50^{2}) \times 200 \times 10^{3} + 50^{2} \times 100 \times 10^{3})}$

$= 24.72 M P a$

単位に注意・・・P=100kN=100×10³、E₁=200GPa=200×10³、E₂=100GPa=100×10³

・応力σ₂

式(4)からσ₂を求める。

$σ_{2} = σ_{1} \times \frac{E_{2}}{E_{1}} = \frac{24.72 \times 100 \times 10^{3}}{200 \times 10^{3}}$

$= 12.36 M P a$

式(7)に中空パイプAの数値を代入し、圧縮量を求める。

$λ ＝ \frac{l}{E_{1}} \times σ_{1} ＝ \frac{400 \times 24.72}{200 \times 10^{3}}$

$= 0.05 m m$

解

中空パイプAの応力：24.72MPa

丸棒Bの応力：12.36MPa

圧縮量：0.05mm

圧縮荷重の面白い話

圧縮荷重に関連した面白いエピソードの一つで、古代ローマの建築技術に関する話があります。

ローマ帝国では、当時圧縮荷重を利用したアーチ構造が好んで採用され、ドーム型の建築技法が非常に発展してしました。特にローマのパンテオンという神殿がその代表例です。この建物は直径約43メートルの巨大なドームを持ち、中央には開口部オルクス(ラテン語で「眼」という意味)があります。このドームは圧縮荷重を巧みに利用しており、重力を均等に分散させることができる構造となっています。

面白いのは、パンテオンのドームが2000年以上も崩れることなく存在している点です(正確に言うと一度火事によって消失し、ハドリアヌス帝が紀元118年から125年にかけてパンテオンを再建設したそうです)。これはローマの建築家たちが圧縮荷重の原理を理解していて、非常に強い材料（例えば、軽量の火山灰を混ぜたコンクリート）を使って設計したためです。

圧縮荷重の理解とその応用が、古代の建築技術において重要な役割を果たし、今でもその影響を感じることができるのは非常に興味深いですね。ちなみにこのパンテオンはローマ市内のマルス広場にあり、今でも観光名所として多くの人々に親しまれています。

圧縮応力の応用が見られるパンテオン宮殿

よかったらシェアしてね！

URLをコピーしました！

URLをコピーしました！