本記事では、支点反力の計算からせん断力図（SFD）と曲げモーメント図（BMD）の描き方を丁寧に解説しています。
初心者の方から復習として活用したい方まで、どなたでも役立つ内容になっています。
具体的な図示方法も交えながら分かりやすく説明していますので、ぜひ参考にしてください！
せん断力図（SFD）とは？
最初にSFD図についてご紹介します。
せん断力図(SFD：Shear Force Diagram)は、はりにかかるせん断力(Shear Force)の変化を、はりの長さに沿って視覚的に分かりやすくグラフ化したものです。
主に建築や土木分野で、構造物がどのように力を受けているかを視覚的に理解するために使われます。
はりがどのように力を受けているかを一目で見て分かるようにするために使われる方法で、以下のような特徴があります。
せん断力図の特徴
- 横軸は梁の長さ、縦軸はせん断力を表します。
- 梁にかかる荷重（重りや力）の影響で、せん断力がどこでどれだけ発生しているかがこの図を見るだけでわかります。
- 荷重が変わるポイント(集中荷重や分布荷重)では、グラフの形が変化します。
曲げモーメント図（BMD）とは？
曲げモーメント図(BMD：Bending Moment Diagram)は、はりにかかる曲げモーメント(Bending Moment)の変化を、梁の長さに沿ってグラフ化したものです。
こちらも同じく、建築や土木分野で構造物の安全性を確認するために使用されます。
曲げモーメント図の特徴
- 横軸は梁の長さ、縦軸は曲げモーメントを表します。
- せん断力図（SFD）の傾きが曲げモーメント図の形に影響します。
- 荷重や支点位置に応じて、曲げモーメントの大きさと力の分布が変わります。
集中荷重が発生している両端支持はりの作図の流れ
ここでは、集中荷重が１つかかっている両端支持はりを例にせん断力図と曲げモーメント図を作っていきます。具体的には、以下のような流れで作図していきます。
- 支点反力の計算
- せん断力図（SFD）の作成
- 曲げモーメント図（BMD）の作成
せん断力図（SFD）の書き方
例えば次のような図で、両端支持はりに集中荷重W(600N)がかかっているはりがあるとします。
この図をもとに、せん断力図を描いていきたいと思います。
それぞれ順番に見ていきましょう。
これが決まらないとせん断力図が書けないので、まずはココから。支点反力RBは、
$$R_{B}=\frac{Wl_{1}}{l}=\frac{600×100}{300}=200N$$
そしてRAは、
$$R_{A}=W-R_{B}=600-200=400N$$
となります。
次に部材断面の正負の定め方についてです。
例えば、はり部材のAC間の区間に注目して、それぞれの力のかかり方を見てみるとこのようになっているかと思います。
ここだけ見ると、このはりは時計回りに回転させられそうな力のかかり方をしていますよね。
一方で、CB間の区間はというと、
コッチは反時計回りに回転しそうに見えますね。
この時計周りor反時計回りにはりが回転しそうだなというのが重要で、材料力学では基本的に時計回りに回転する力の方向(左側：鉛直上向きの荷重、右側：鉛直下向きの荷重)を正(＋)と置き、その逆の反時計回りの力の向きを負(－)と決め、せん断力図を作成していきます。
ということでここでは、
AC間のはり部材：+400N
CB間のはり部材：－200N
となります。
先ほど、はり部材のAC間：+400N、CB間：－200Nということが分かったので、これをせん断力図に落とし込んでいきます。するとこのような図ができます。
ちなみに集中荷重がかかっているC点ではせん断力が急激に変化していますが、これはゼロNになるのではなく、前後で値が異なるということを表しています。
次は、曲げモーメント図の作図に移っていきます。
曲げモーメント図（BMD）の書き方
曲げモーメント図は、モーメントの公式を使って求めていきます。力のモーメントは、
$$M(モーメント)=F(力)×L(腕の長さ)$$
で求められましたね。
この式をもとにしてそれぞれの曲げモーメントを算出していきます。
そして、せん断力図と同様に、曲げモーメントの正負の符号があります。図で表すとこのようになります。
今回の場合、集中荷重が発生している箇所で曲げモーメントが最大となり、左右両端では曲げモーメントはゼロになります。支点Aから任意の位置にある仮想断面をXとしておいて計算すると、次のように求められます。
- A点の曲げモーメント(X=0のとき)
$$M_{AC}=R_{A}×X=400×0=0Nmm$$ - C点の曲げモーメント(X=100のとき)
$$M_{C}=R_{B}×(l-X)=200×(300-100)=200×200=40,000Nmm$$
または、
$$M_{C}=R_{A}×X=400×100=40,000Nmm$$ - B点の曲げモーメント(X=300のとき)
$$M_{BC}=R_{B}×(l-X)=200×(300-300)=0Nmm$$
そして、図を描くとこのようになります。
以上より、この手順で計算していけば、せん断力図（SFD）と曲げモーメント図（BMD）を作図することができます。
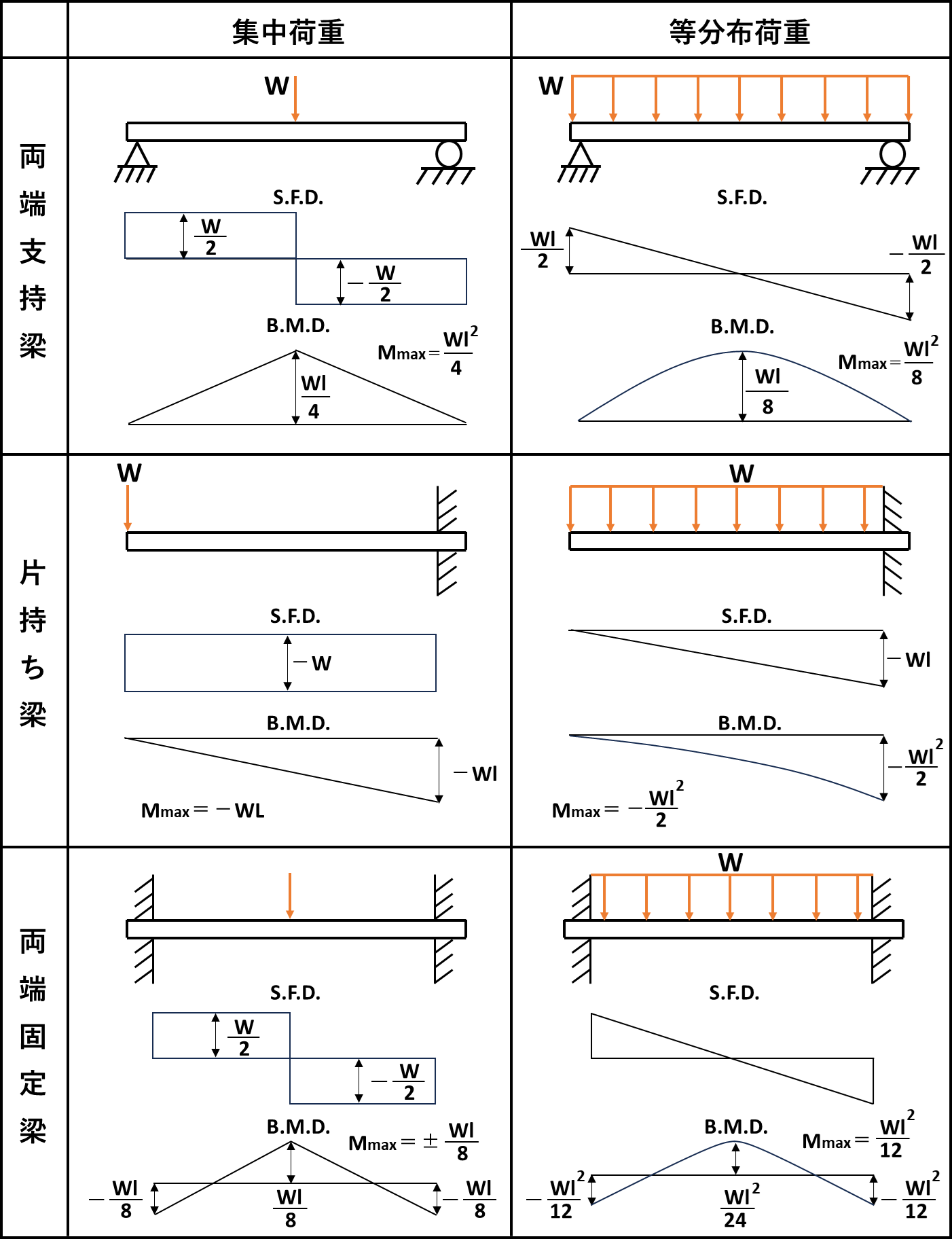
【参考】せん断力図と曲げモーメント図一覧
せん断力図と曲げモーメント図の書き方については、荷重のかかり方によって変わってきます。
以下の表は荷重条件ごとのせん断力図（SFD）と曲げモーメント図（BMD）の荷重の分布をまとめたものです。
まとめ
今回は、集中荷重が１つかかっている両端支持はりを例に、計算と作図方法をご紹介しました。
はりの問題をマスターするには、自分で荷重の数値を変えたり、荷重のかかり方をアレンジして解いていくと理解しやすいかと思います。
今回の内容は材力の基本問題ともいえる内容なので、ココが分かれば複雑な問題にも対応できるようになり、よりロジカルな考え方が力が身につくでしょう。
次回は複数の荷重がかかる場合や、異なる支持条件を持つはりについても詳しく解説していきたいとおもいます。
ぜひ、次回もお楽しみに！