この記事では、はりなどの構造部材を安全かつ効率的に設計するうえで欠かせない断面二次モーメントIと断面係数Zの基本的な考え方や算出手順を、具体例を交えながら詳しく解説していこうと思います。
断面係数は部材に作用する曲げ応力を正確に評価するうえで重要なパラメータであり、特に材料力学においては形状や寸法が異なるさまざまな断面に対し、柔軟に対応して計算できることが求められます。
そこで本記事では、長方形断面や円形断面といった代表的な例を中心に、断面係数を算出するうえで押さえるべきポイントや注意点を分かりやすく紹介します。
また、建築・土木・機械など多岐にわたる分野での活用も視野に入れていますので、初学者から実務者まで幅広い方に役立つ内容となっています。
ぜひ、今回の記事を参考にしてみてください。
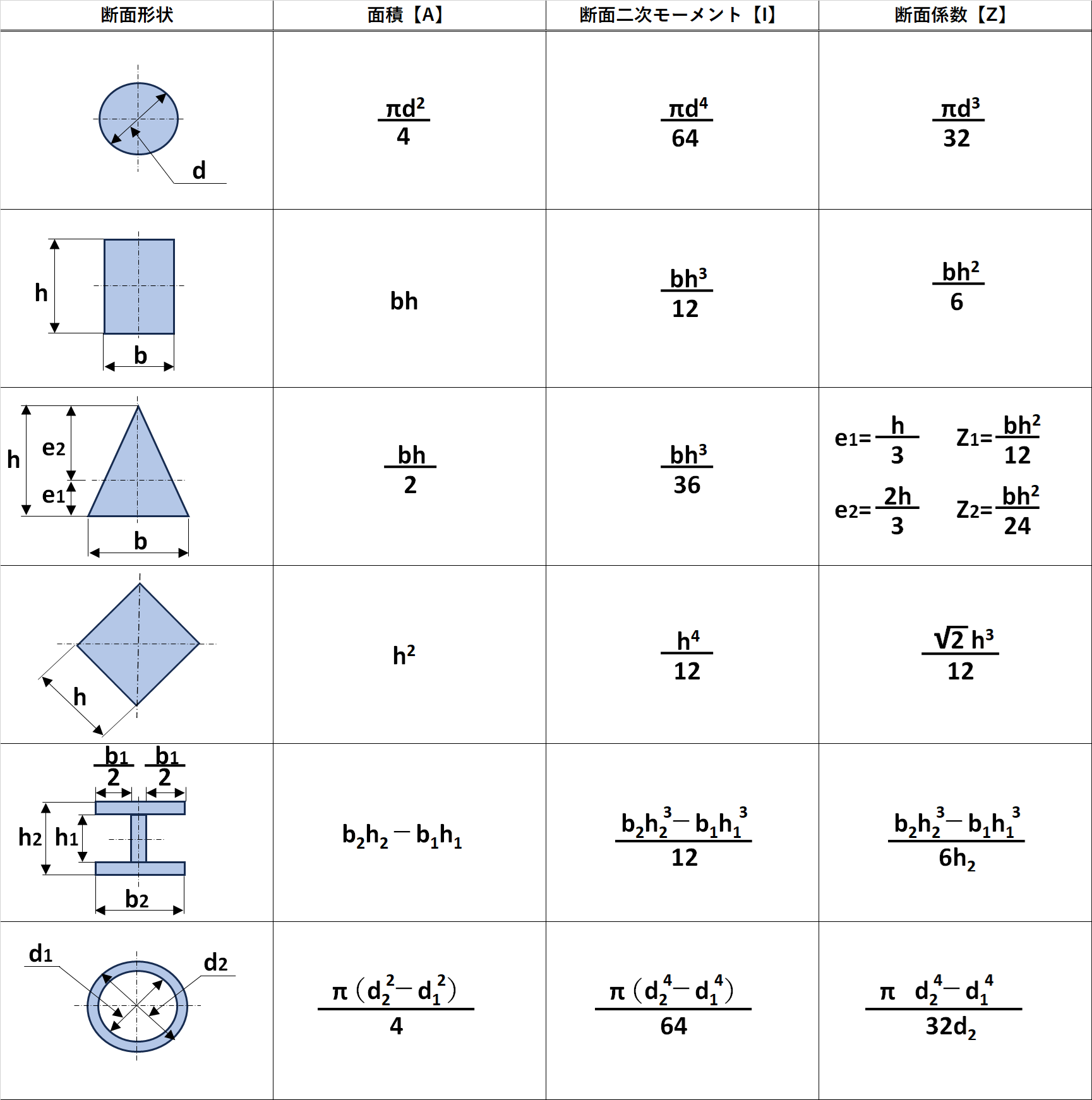
断面二次モーメントと断面係数の一覧
この記事では、以下の代表的な断面二次モーメントとその断面係数を用いて、断面係数Zを具体的に計算していく内容となります。
加減算を使って断面二次モーメント$I$を計算
断面二次モーメントは、基本的な形状の断面二次モーメントを組み合わせて計算することができます。
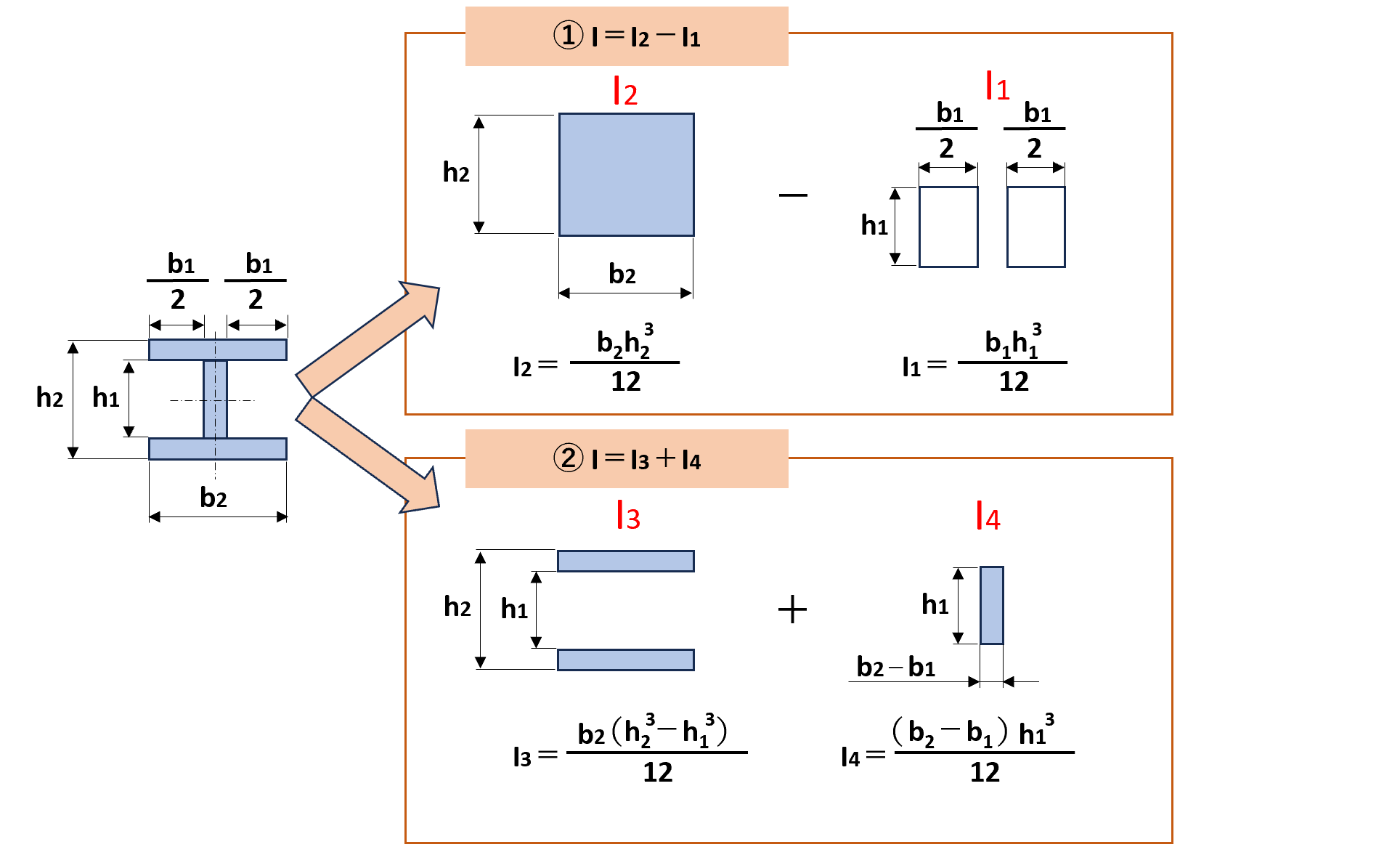
例えば、$I$型の形状を持つ材料の断面二次モーメント$I$は、
$$I=\frac{b_{2}h_{2}^3-b_{1}h_{1}^3}{12}$$
となります(上の図を参考)。
この材料の形状を例にとって説明すると、今回の$I$型の形状を持つ材料は2つの計算方法によって断面二次モーメント$I$を算出できます。
ではどのように計算していけばよいのか、以下に具体的な計算手順を記載しましたので、見ていきましょう。
①長方形の$I_{2}$から2つの長方形の$I_{1}$を引いたもの($I=I_{2}-I_{1}$)
単刀直入に言うと、
$$I=I_{2}-I_{1}$$
という式に見立てて計算していく方法です。
ここで、このように計算する際、長方形断面の断面二次モーメント(曲げ剛性を表す量)$I$の標準公式は、
$$I= \frac{bh^{3}}{12}$$
なので、これを使います。今回の断面については、「大きな長方形から中抜きした長方形を差し引く」形で表せますが、どちらも
$$I= \frac{幅×高さ^{3}}{12}$$
の形を用いて求めます。
具体的には、
$$大きい方の長方形部分I_{2}:\frac{b_{2}h_{2}^{3}}{12}$$
$$小さい方の長方形部分I_{1}:\frac{b_{1}h_{1}^{3}}{12}$$
と表し、これを先ほどの$I=I_{2}-I_{1}$にあてはめると、
$$I=I_{2}-I_{1}$$
$$\frac{b_{2}h_{2}^{3}}{12}-\frac{b_{1}h_{1}^{3}}{12}$$
$$I=\frac{b_{2}h_{2}^3-b_{1}h_{1}^3}{12}$$
と計算できます。
②2つの長方形の$I_{3}$と、1つの長方形の$I_{4}$を加えたもの($I=I_{3}+I_{4}$)
もうひとつの計算方法は、
$$I=I_{3}+I_{4}$$
という方法を使います。
このときの分割方法のイメージとしては、ざっくり次の 3 つのパーツ(長方形)に分けて考えていくことです。
横長断面$I_{3}$
上と下の横長断面だけを見た場合、このように式を立てられます。
$$I= \frac{b_{2}(h_{2}^{3}-h_{1}^{3})}{12}$$
縦長断面$I_{4}$
縦長断面だけを見た場合の断面二次モーメント$I$は、
$$I= \frac{(b_{2}-b_{1})h_{1}^{3}}{12}$$
とあらわせます。
$I_{3}$と$I_{4}$を合算
これらを先ほどの$I=I_{3}+I_{4}$にあてはめると、
$$I=I_{3}+I_{4}$$
$$= \frac{b_{2}(h_{2}^{3}-h_{1}^{3})}{12}+ \frac{(b_{2}-b_{1})h_{1}^{3}}{12}$$
$$= \frac{b_{2}h_{2}^{3}-b_{2}h_{1}^{3}}{12}+ \frac{b_{2}h_{1}^{3}-b_{1}h_{1}^{3}}{12}$$
$$= \frac{b_{2}h_{2}^{3}-b_{2}h_{1}^{3}+b_{2}h_{1}^{3}-b_{1}h_{1}^{3}}{12}$$
$$= \frac{b_{2}h_{2}^{3}-b_{1}h_{1}^{3}}{12}$$
となります。
なお、このように加減算が可能な理由は、重ね合わせの原理を利用しているためです。
断面二次モーメントは、ある軸に対する形状とその面積分布に基づいた量であるため、複数の形状に切り分けて断面二次モーメントを加算・減算して求めることができます。
また、形状が異なる場合でも、同じ軸に対してそれぞれの断面二次モーメントを求め、座標系をそろえて(場合によっては平行軸の定理を用いて)合成するという方法でも計算できます。
断面二次モーメント$I$、断面係数$Z$の関係
次は、断面二次モーメントと断面係数の関係についてです。
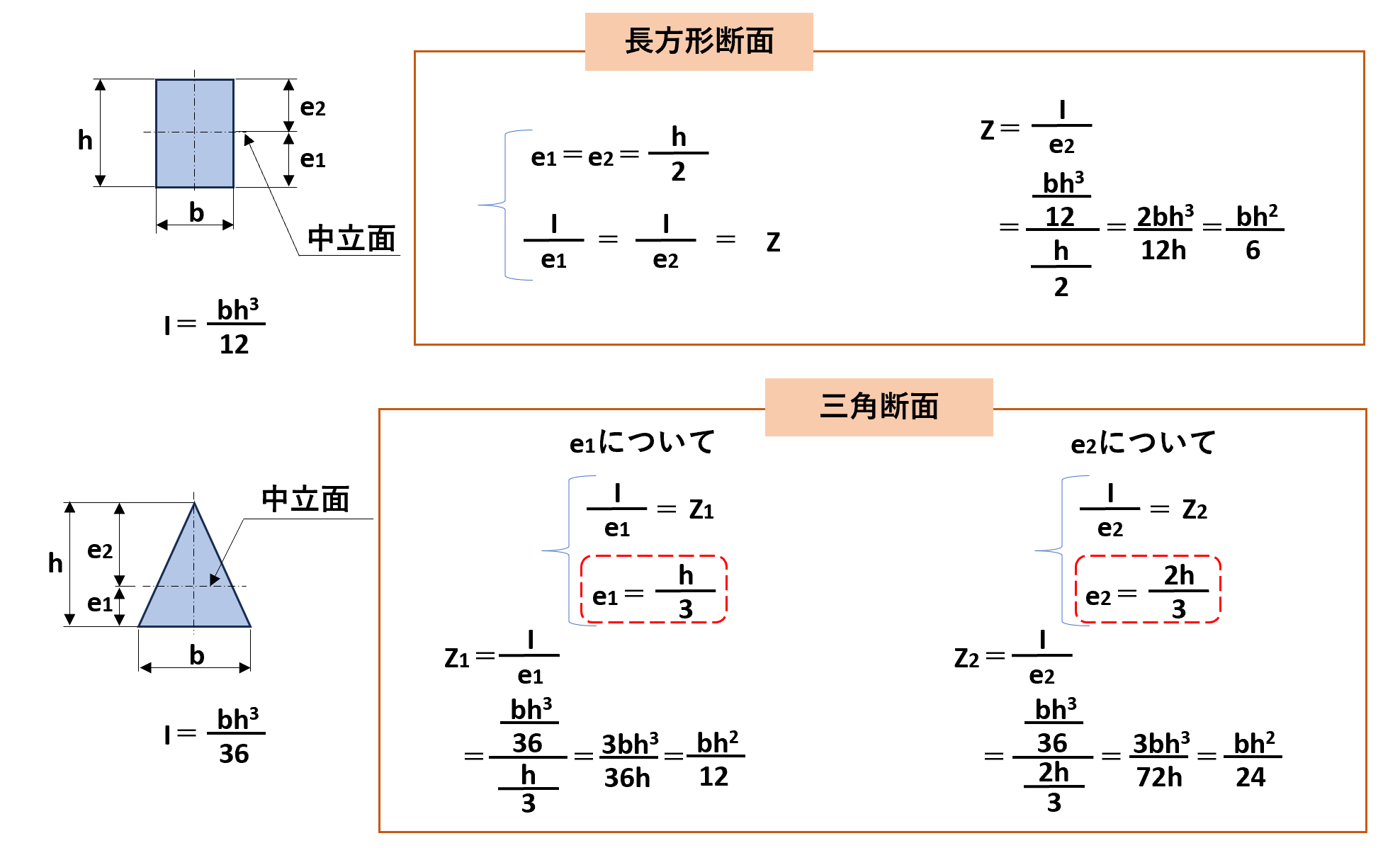
断面係数Zは、断面二次モーメント$I$を中立面からの距離で割って得られる係数です。
長方形断面のような形状は、中立面から引張側と圧縮側それぞれ両表面までの距離(e1、e2)は等しいのですが、下記の三角断面のような中立面から引張・圧縮両表面までの距離が異なる場合は、それぞれの断面係数(e1、e2)が異なります。
こちらも、順番に見ていきましょう。
断面が上下対称である場合
例えば、長方形断面のような形状の場合、断面形状が上下対称であることから中立面から引張側と圧縮側の両表面までの距離(e1、e2)は等しいです。
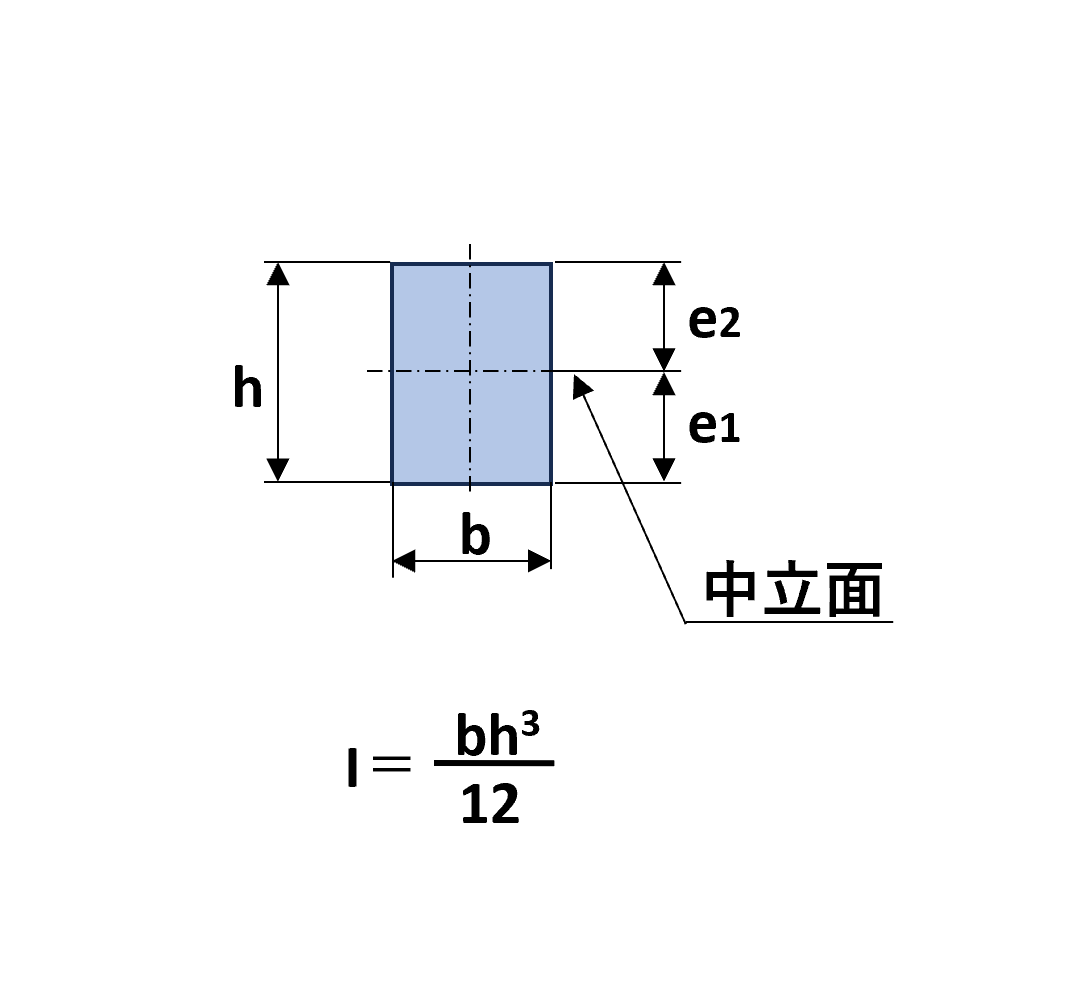
これを式で表すと、
$$e_{1}=e_{2}=\frac{h}{2}$$
と表せます。
同様に、断面係数Zもそれぞれ等しいので、
$$\frac{I}{e_{1}}=\frac{I}{e_{2}}=Z$$
と表せます。
これを断面係数Zについて計算すると、
$$Z=\frac{I}{e_{2}}$$
$$=\frac{\frac{bh^{3}}{12}}{\frac{h}{2}}$$
$$=\frac{2bh^3}{12h}$$
$$=\frac{bh^2}{6}$$
とZを算出できます。
断面が上下非対称である場合
一方で、三角断面のような中立面から引張・圧縮両表面までの距離が異なる場合は、それぞれの断面係数(e1、e2)が異なります。
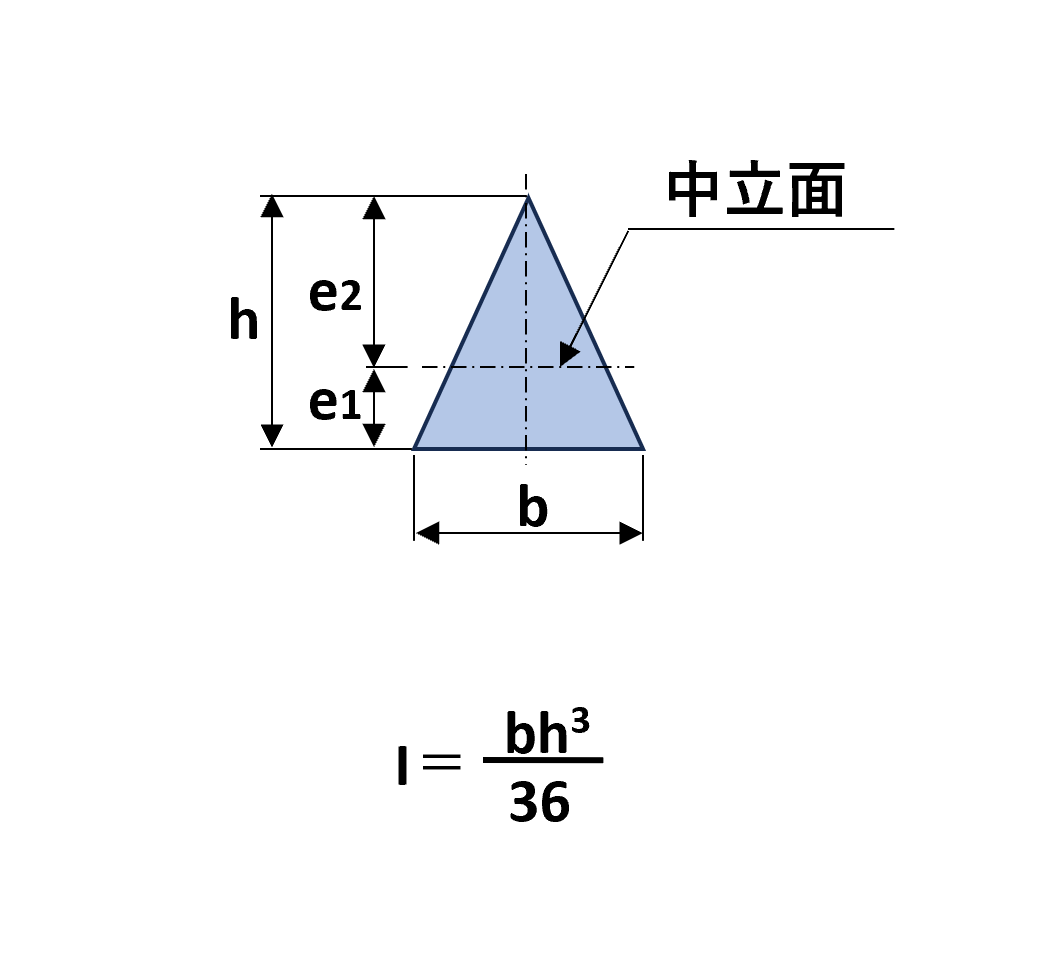
断面係数e1とe2それぞれを順番に計算すると以下のようになります。こちらも順番に見ていきましょう。
断面係数e1について
三角形状の場合、断面係数e1は、
$$e_{1}=\frac{h}{3}$$
となります。また、断面係数Zは、
$$Z_{1}=\frac{I}{e_{1}}$$
であることから、
$$Z_{1}=\frac{I}{e_{1}}$$
$$=\frac{\frac{bh^3}{36}}{\frac{h}{3}}$$
$$=\frac{3bh^3}{36h}$$
$$=\frac{bh^2}{12}$$
となります。
断面係数e2について
一方で、断面係数e2は、
$$e_{2}=\frac{2h}{3}$$
となります。また、断面係数Zは、
$$Z_{2}=\frac{I}{e_{2}}$$
であることから、
$$Z_{2}=\frac{I}{e_{2}}$$
$$=\frac{\frac{bh^3}{36}}{\frac{2h}{3}}$$
$$=\frac{3bh^3}{72h}$$
$$=\frac{bh^2}{24}$$
となります。
なぜ、断面係数(e1、e2)が異なるのか?
この現象は、そもそも断面形状が左右対称・上下対称でない場合に起こるものです。
長方形断面など軸対称の場合には、圧縮側表面(上側)と引張側表面(下側)までの距離が同じなので、
$$e_{1}=e_{2}$$
となり、断面係数Zも1つで表せます。
しかし、形状が左右(もしくは上下)非対称であれば、その重心軸(中立軸)が断面の幾何学的中心(見た目の中央)にこない場合が多々あります。
これにより、上側と下側(あるいは左側と右側)までの距離が違ってくる、というわけです。
以上の内容を把握したところで、ここから先は演習問題に取り組んでいきたいと思います。
計算問題
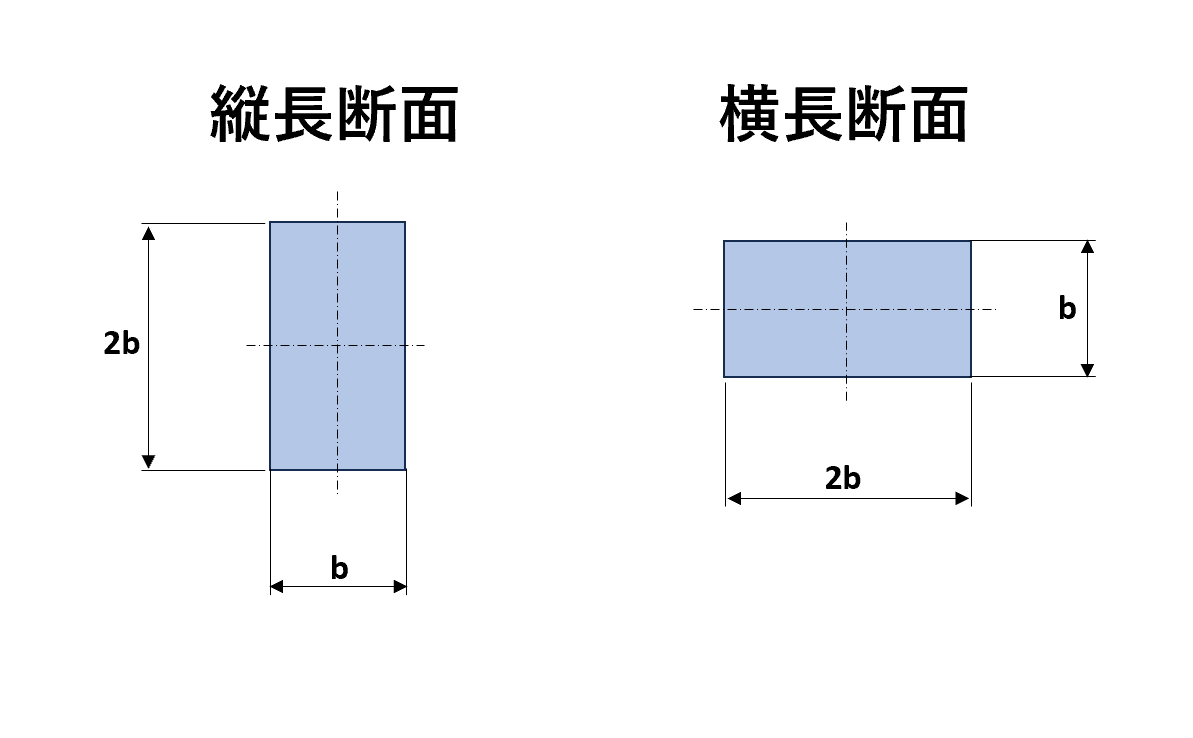
例題1
辺の長さ1:2の長方形の部材があるとする。この部材は、曲げ荷重に対して横長よりも縦長で使用したほうが強いと考えます。この理由を説明しなさい。
例題1の解答
はりが強いということは、一定の曲げモーメントMに対して、発生する曲げ応力σが小さいこととします。
このことから、曲げモーメントMが一定ならば、σの大きさは断面係数Zに反比例します。
式で表すと、
$$σ=\frac{M}{Z}$$
となります。
ここで、縦長断面の断面係数をZ1、横長断面の断面係数をZ2と置き、両者の断面係数を比較します。
①縦長断面の場合
$$Z_{1}=\frac{b(2b)^2}{6}$$
$$=\frac{4b^3}{6}$$
②横長断面の場合
$$Z_{2}=\frac{2bb^2}{6}$$
$$=\frac{2b^3}{6}$$
③縦長断面の場合と横長断面の場合を比較
$$\frac{Z_{1}}{Z_{2}}$$
$$=\frac{\frac{4b^3}{6}}{\frac{2b^3}{6}}$$
$$=2$$
この式から、Z1はZ2の2倍になり、縦長断面に発生する応力は、横長断面の$\frac{1}{2}$の力しか作用しないことが分かります。
このことから、横長よりも縦長で使用したほうが強度のある材料になります。
例題2(実務・応用編)
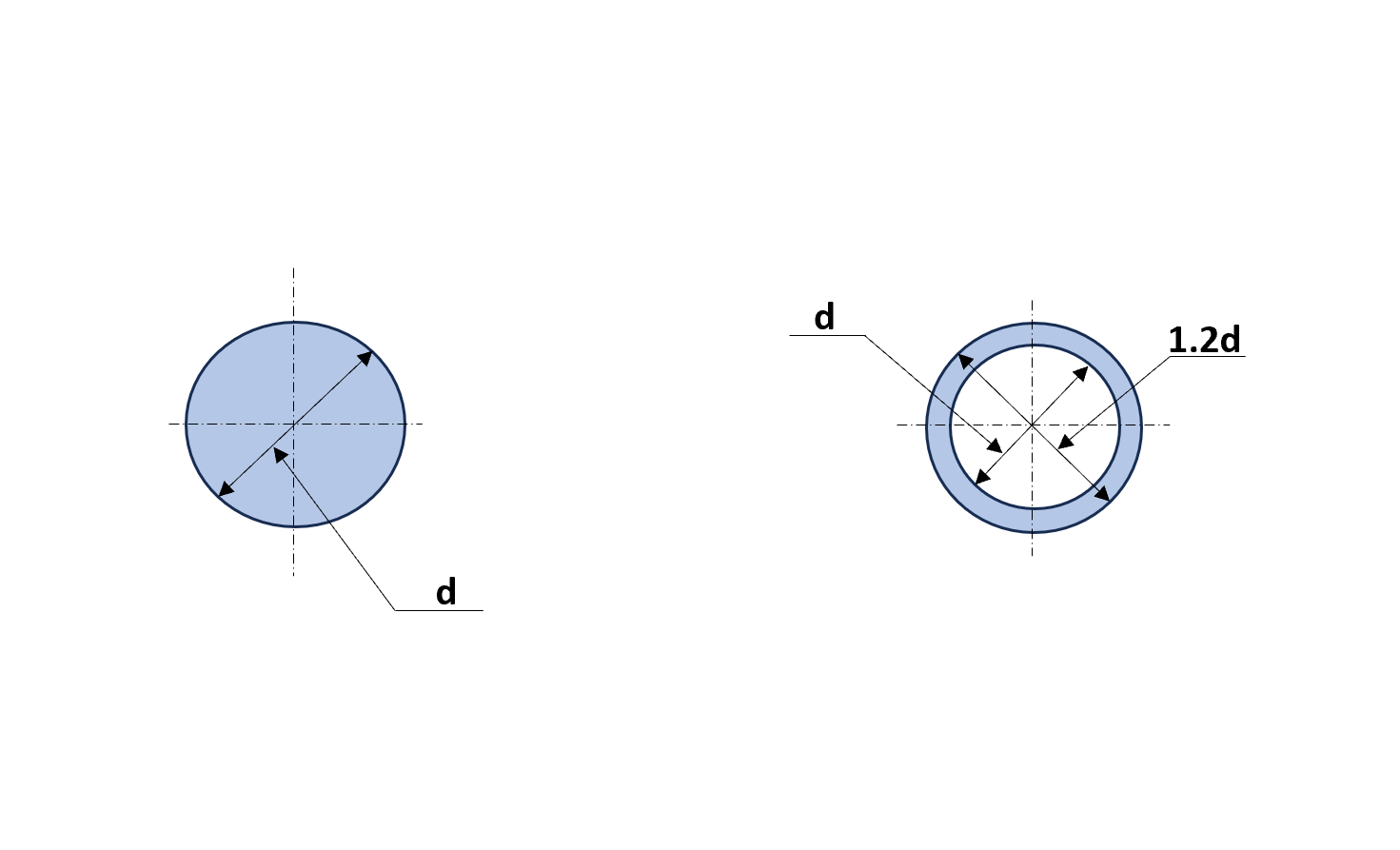
直径dの丸棒と内径d、外径が1.2dの薄肉パイプがあるとします。この2つの断面係数を計算し両者を比較しなさい。
例題2の解答
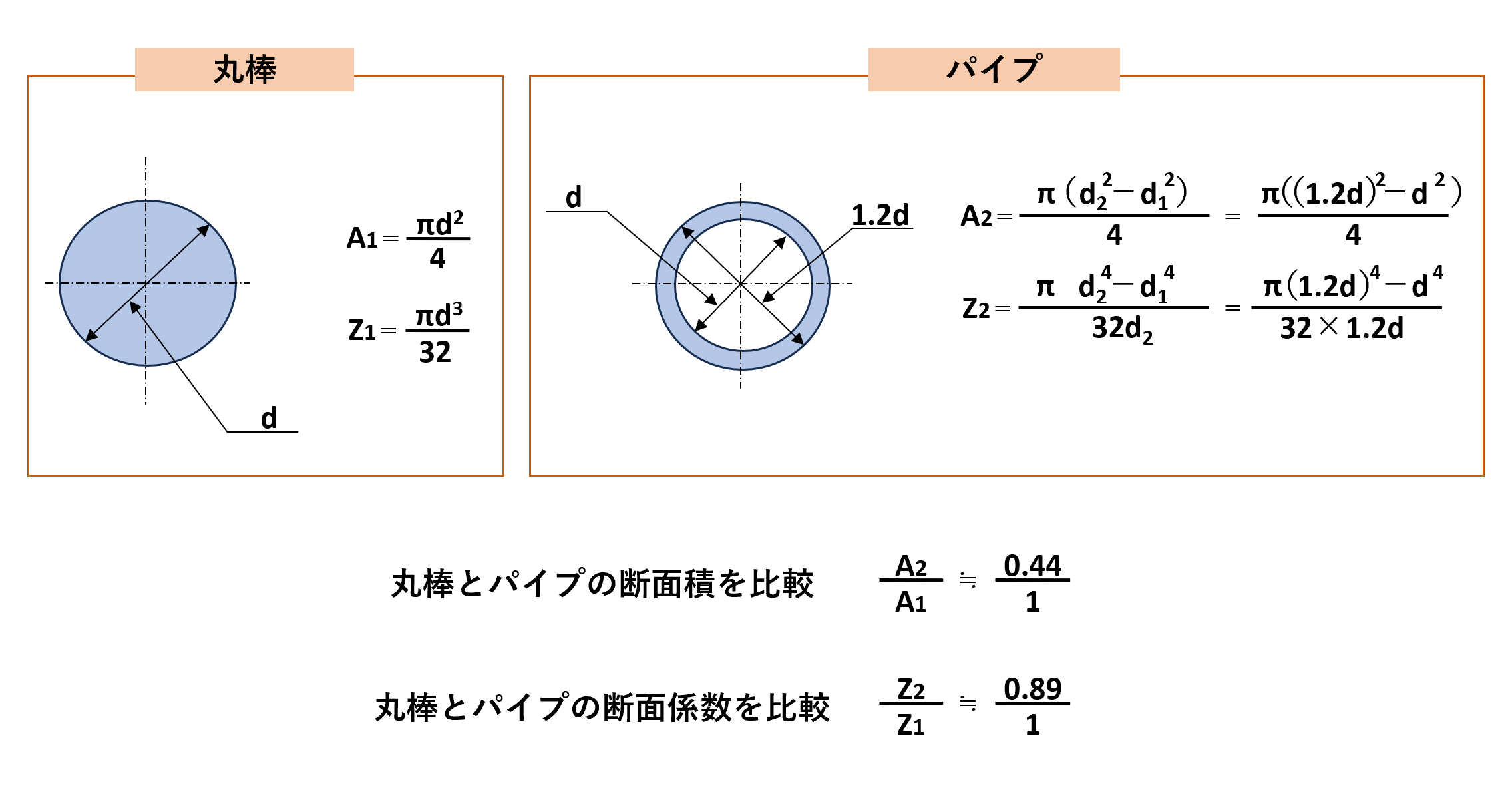
丸棒とパイプの断面係数を比較する前に、まずはそれぞれの断面積と断面係数を確認します。
直径dの丸棒
断面積A1
$$A_{1}=\frac{πd^2}{4}$$
断面係数Z1
$$Z_{1}=\frac{πd^3}{32}$$
外径が1.2dの薄肉パイプ
断面積A2
$$A_{2}=\frac{π(d_{2}^2-d_{1}^2)}{4}$$
$$=\frac{π((1.2d)^2-d^2)}{4}$$
断面係数Z2
$$Z_{2}=\frac{πd_{2}^4-d_{1}^4}{32d_{2}}$$
$$=\frac{π(1.2d)^4-d^4}{32×1.2d}$$
丸棒とパイプの断面係数を比較
丸棒Z1とパイプZ2を比率で表します。
$$\frac{Z_{2}}{Z_{1}}≒\frac{0.89}{1}$$
このことから、薄肉パイプは丸棒に対して、曲げ強さで約90%の値を持っていることが分かります。
丸棒とパイプの断面積を比較
次は、丸棒とパイプの断面積を比較します。
$$\frac{A_{2}}{A_{1}}≒\frac{0.44}{1}$$
このことから、薄肉パイプは丸棒に対して、面積比(重量比)では約45%の値を持っていることが分かります。
解:薄肉パイプは丸棒に対して曲げ強さで約90%、面積比(重量比)では約45%の値を持つ。
まとめ
本記事では、断面二次モーメントIと断面係数Zの基本概念や計算手順を、長方形断面や三角断面を例に分かりやすく解説しました。
これらのパラメータは、はりなどの構造部材の曲げ応力を正確に評価するうえで欠かせない要素です。形状や寸法によって計算方法はさまざまですが、ポイントさえ押さえれば柔軟に対応できます。
また、建築・土木・機械といった多岐にわたる分野でも共通して用いられるため、専門分野が異なっていても理解しておくことが非常に大切です。今回ご紹介した基本的な考え方を踏まえて、ご自身の分野や実務でもぜひ役立ててみてください。
