はりは荷重を受ければ必ずしなります。
肉眼ではわずかな曲がりでも、設計の世界では“致命的”な誤差につながることがあります。
強度を語るうえでよく登場する断面係数や許容応力は、あくまで“壊れにくさ”の指標であって、“どこまで曲がるか”は別問題となります。ここを見落とすと、例えば扉が閉まらない・部品が噛み合わないといった不具合が発生し、クレームへ直結しかねません。
この記事では、そんな見過ごされがちな「たわみ量」を主役に据え、実務で使える係数β・αの使い方から計算方法まで掘り下げます。
一緒にマスターしていきましょう。
たわみとは?
はりは基本的に外力を受けると内部に曲げモーメントが発生し、その結果として形状がわずかに湾曲します。
このような現象のことを材料力学では「たわみ」と呼びます。
たわみは、部材内部で生じる圧縮応力と引張応力の各層が連続して積み重なり、変形エネルギーとして外部に現れるものです。
この大きさは、荷重の種類・大きさ・分布、材料のヤング係数 (E)、そして断面形状によって決まる曲げ剛性 (EI) に強く依存します。言い換えると、断面係数やはりの強度(耐力)だけを評価しても、部材がどれだけたわむかという変形量は判断できないということになります。
はりのたわみについて
外力により中立軸が曲線を描く現象がたわみであり、荷重を受けて変形したはりの中立面に沿って描く曲線部分のことを「たわみ曲線」といいます。
中立面上の任意の点Cからその変位C’までの間隔をたわみδ(デルタ)と呼び、点C’の接線をたわみ角$i$と呼びます。
片持ちはりでは、自由端のたわみが最大たわみ、自由端のたわみ角が最大たわみとなります。
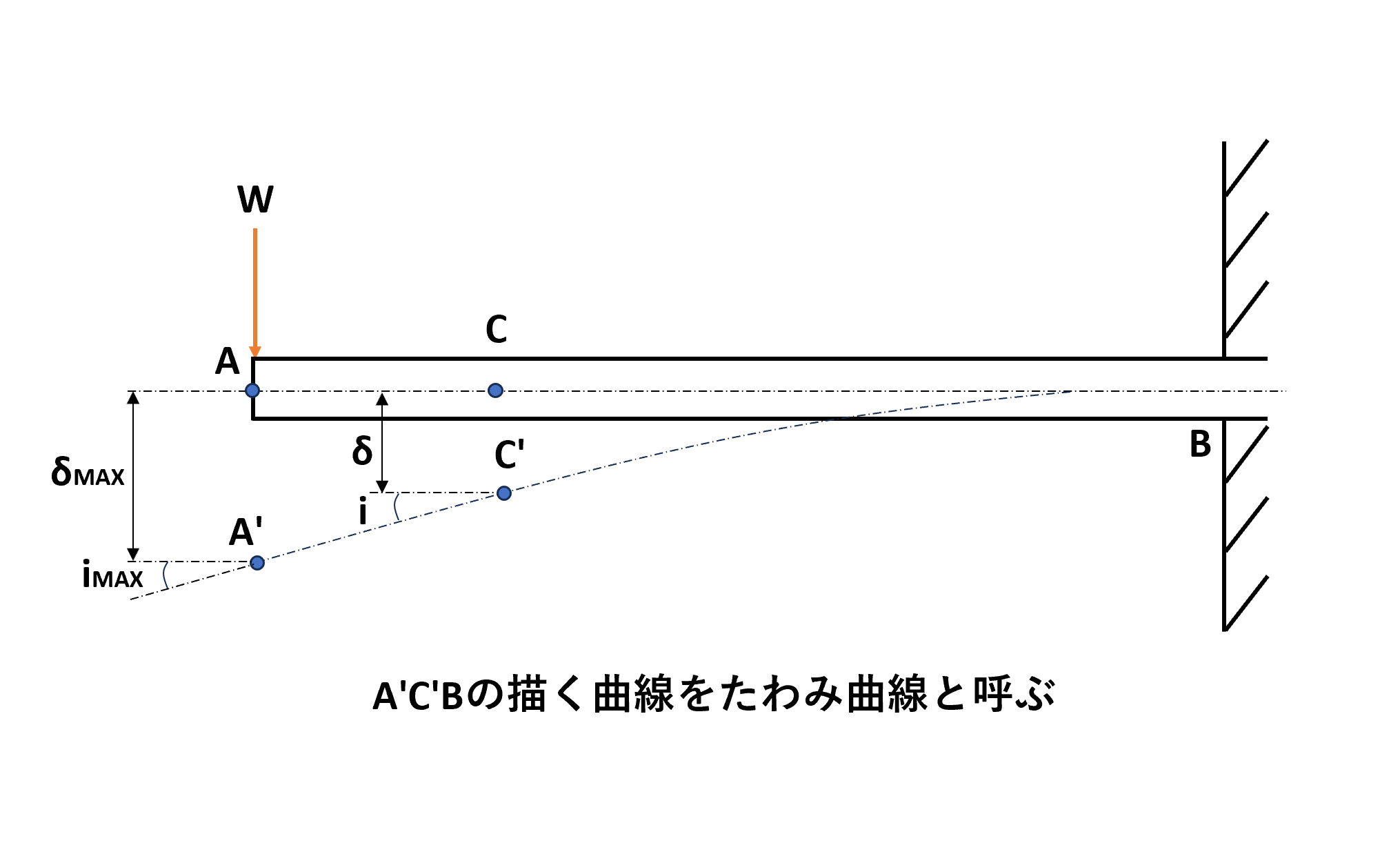
上記の図より、
任意の点(点C)では、
$$δ:たわみ$$
$$i:たわみ角$$
自由端では、
$$δ_{max}:最大たわみ$$
$$i_{max}:最大たわみ角$$
と定義しています。
また、たわみ角の単位はradで表します。
最大たわみδmaxと最大たわみ角imax
はりのたわみ変形は、はりの種類と荷重条件によって大きく異なります。そこで、代表的なはりに対して、図に示す係数を与えて、次の一般式でたわみとたわみ角を求めます。
最大たわみ
$$δ_{max}=β\frac{Wl^3}{EI}$$
最大たわみ角
$$i_{max}=α\frac{Wl^2}{EI}$$
※たわみ角の単位はradで表します。
$W:荷重$
$l:はりの長さ$
$E:縦弾性係数$
$I:断面二次モーメント$
$EI:曲げ剛性$
$α:たわみ角の係数$
$β:たわみ係数$
たわみの係数とたわみ角一覧図
上記の最大たわみδmaxと最大たわみ角imaxは、はりの支持形式によって適用する係数(α・β)が異なります。
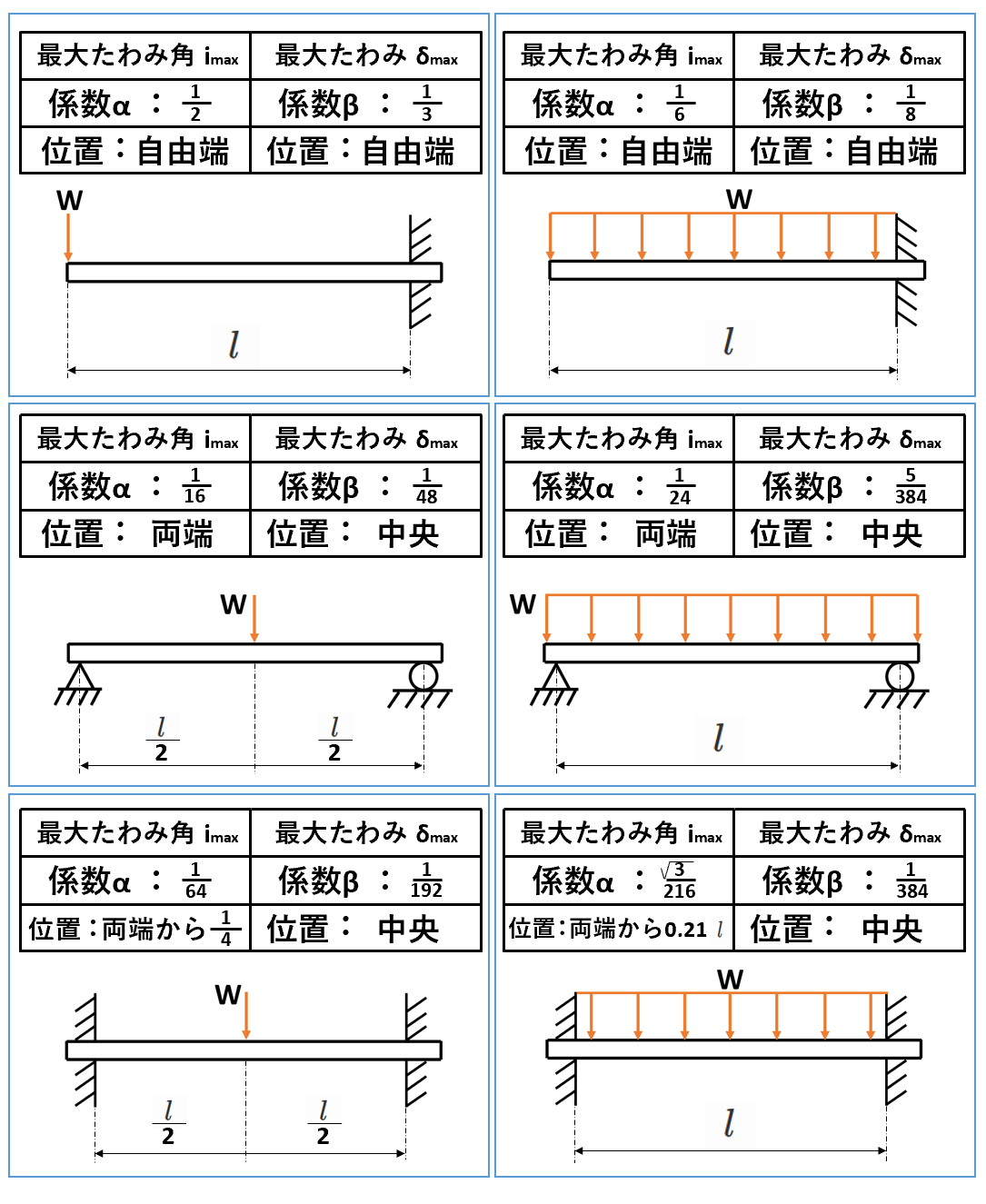
たわみ係数βとたわみ角係数α
たわみの計算方法は、材質によって決まる縦弾性係数と、形状から決定される断面二次モーメントを使って求めていきます。
はりの曲げ変形は「支持条件」と「荷重のかけ方」で大きく変わります。微分方程式から解くこともできますが、実務ではあらかじめ支持形式に応じたたわみ係数 βとたわみ角係数 αを覚えておくと、パッと答えが出すことができます。
| $$計算式$$ | $$意味$$ |
|---|---|
| $$δ_{max}=β\frac{Wl^3}{EI}$$ | $$荷重 W で生じる最大たわみ (mm)$$ |
| $$i_{max}=α\frac{Wl^2}{EI}$$ | $$代表点(任意の位置)での最大たわみ角 (rad)$$ |
最大たわみと最大たわみ角は、数値が小さいほどたわみにくく、変形が小さくなるなります。
例題1
図のような形状の材料の最大たわみと最大たわみ角を求めなさい。縦弾性係数は206GPaとします。
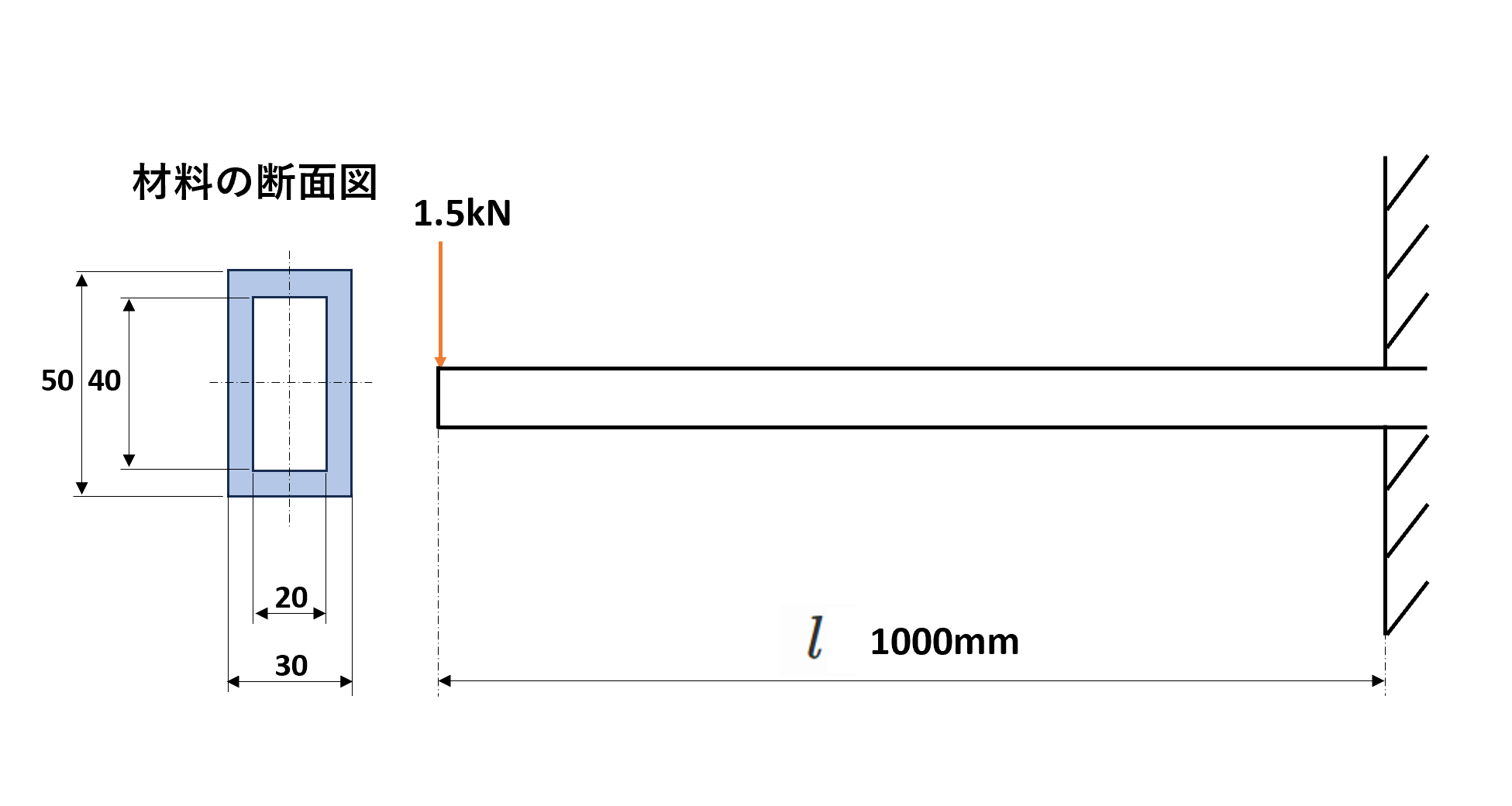
ポイント
材料の形状・荷重・スパン長・縦弾性係数がすでに分かっている問題なので、最大たわみと最大たわみ角の式をそのまま使えます。しかし、断面二次モーメント$I$だけわからないので、まずはこの$I$から計算していきます。
例題1の解答
断面二次モーメント$I$
$$I=\frac{1}{12}(b_{2}h_{2}^3-b_{1}h_{1}^3)$$
$$=\frac{b_{2}h_{2}^3-b_{1}h_{1}^3}{12}$$
$$=\frac{30×50^3-20×40^3}{12}$$
$$=205833.33mm^4$$
$$=2.06×10^5mm^4$$
最大たわみ角
最大たわみ角を求めるのに必要な係数αは、先ほどの表から、
$$たわみ角の係数α=\frac{1}{2}$$
となる。この係数を使って計算すると、
$$i_{max}=α\frac{Wl^2}{EI}$$
$$=\frac{1}{2}×\frac{1500×1000^2}{206×10^3×2.06×10^5}$$
$$=0.0176736・・・$$
$$=0.02rad$$
最大たわみ
最大たわみを求めるのに必要な係数βは、先ほどの表から、
$$たわみ係数β=\frac{1}{3}$$
となる。この係数を使って計算すると、
$$δ_{max}=β\frac{Wl^3}{EI}$$
$$=\frac{1}{3}×\frac{1500×1000^3}{206×10^3×2.06×10^5}$$
$$=11.782448・・・$$
$$=11.78mm$$
解:最大たわみは11.78mm、最大たわみ角は0.02rad
例題2(断面係数を求める問題)
図のようなはりの最大たわみを3mm、許容曲げ応力σを50MPaとしたい。その場合の断面寸法bを求めなさい。縦弾性係数は206GPaとします。
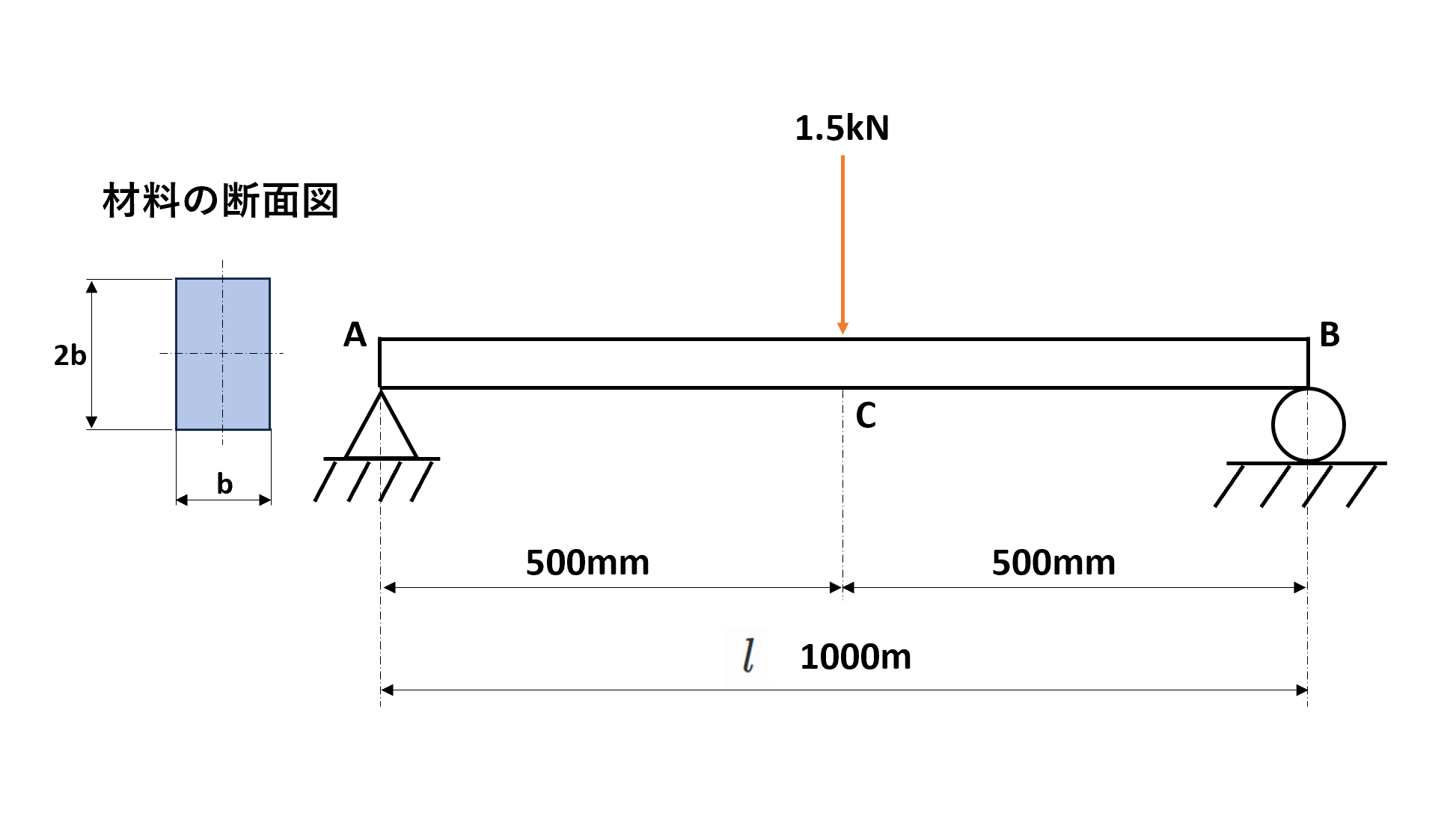
ポイント
断面寸法bの求め方は、①はりのたわみと②曲げ応力の2つの条件から計算できます。そこで、それぞれを計算してみて、大きな数値(安全寄りの数値)を採用するという方法をとります。
例題2の解答
たわみの式から断面寸法bを求める
①断面二次モーメント
$$断面二次モーメントI=\frac{1}{12}bh^3$$
$$=\frac{1}{12}b(2b)^3$$
$$=\frac{8}{12}b^4$$
②最大たわみ
最大たわみδmaxを求める際に必要なたわみ係数βは、上の表より
$$たわみ係数β=\frac{1}{48}$$
を使います。この係数を使い、最大たわみδmaxを計算すると、
$$δ_{max}=β\frac{Wl^3}{EI}$$
$$=\frac{1}{48}×\frac{Wl^3}{E\frac{8}{12}b^4}$$
$$=\frac{1}{48}×\frac{Wl^3}{\frac{8Eb^4}{12}}$$
$$=\frac{1}{48}×\frac{12Wl^3}{8Eb^4}$$
$$=\frac{12Wl^3}{384Eb^4}$$
$$=\frac{Wl^3}{32Eb^4}$$
上式を、bについて求める式へ変換する。
$$δ_{max}=\frac{Wl^3}{32Eb^4}$$
$$δ_{max}×\frac{32E}{Wl^3}=\frac{\cancel{Wl^3}}{\cancel{32E}b^4}×\frac{\cancel{32E}}{\cancel{Wl^3}}$$
$$\frac{32Eδ_{max}}{Wl^3}=\frac{1}{b^4}$$
$$b^4=\frac{Wl^3}{32Eδ_{max}}$$
$$b=\sqrt[4]{\frac{Wl^3}{32Eδ_{max}}}$$
$$=\sqrt[4]{\frac{1500×1000^3}{32×206×10^3×3}}$$
$$=16.59541・・・$$
$$=16.60mm$$
曲げ応力の式から断面寸法bを求める
①断面係数Z
$$Z=\frac{1}{6}bh^2$$
$$=\frac{1}{6}b(2b)^2$$
$$=\frac{1}{6}b×4b^2$$
$$=\frac{4}{6}b^3$$
②最大曲げモーメントM
$$M=Fl$$
$$=1000×500$$
$$=5×10^5Nmm$$
③曲げ応力
$$σ=\frac{M}{Z}$$
$$=\frac{M}{\frac{4}{6}b^3}$$
$$=\frac{6M}{4b^3}$$
上式を、bについて求める式へ変換する。
$$σ=\frac{6M}{4b^3}$$
$$σ×\frac{4}{6M}=\frac{\cancel{6M}}{\cancel{4}b^3}×\frac{\cancel{4}}{\cancel{6M}}$$
$$\frac{4σ}{6M}=\frac{1}{b^3}$$
$$b^3=\frac{6M}{4σ}$$
$$b=\sqrt[3]{\frac{6M}{4σ}}$$
$$=\sqrt[3]{\frac{6×5×10^5}{4×50}}$$
$$=24.662120・・・$$
$$=24.66mm$$
両者を比較し、大きい数値のほうを採用
たわみの式から断面寸法bを求めると16.60mm、曲げ応力の式から断面寸法bを求めると24.66mmだったので、24.66mmを使う。
解:許容曲げ応力の条件より、断面寸法bは24.66mmにすると最大たわみを3mm、許容曲げ応力σを50MPaにすることができる。
まとめ
ここまで読んでくださってありがとうございます。
係数αとβの扱いさえ間違わなければ、面倒な積分方程式を解かなくても変形量が一瞬でつかめます。
強度チェックだけで安心しちゃうと「扉が閉まらない」なんてオチにもなりかねませんから、必ずたわみも同時にチェックしていきましょう。
今日はここまで、また次回お会いしましょう。
